[题目]设等差数列的公差为.前项和为.记.则数列的前项和是( )A. B. C. D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设等差数列的公差为，前项和为，记，则数列的前项和是（）

A. B. C. D.

【答案】C

【解析】分析: 由等差数列的求和公式可得首项，tanantanan+1=﹣1=﹣1，运用裂项相消求和，结合两角和差的正切公式，即可得到所求和．

详解: 等差数列{an}的公差d为，前8项和为6π，

可得8a1+×8×7×=6π，解得a1=，

tanantanan+1=﹣1=﹣1，

则数列{tanantanan+1}的前7项和为

（tana8﹣tana7+tana7﹣tana6+…+tana2﹣tana1）﹣7

=（tana8﹣tana7）﹣7=（tan﹣tan）﹣7

=（tan﹣tan）﹣7

=（tan（）﹣tan（））﹣7

=（）﹣7= ．

故选C．

点睛:解答本题的关键是化简,求和首先要看通项的特征, tanantanan+1=﹣1=﹣1，化简到这里之后,就可以再利用裂项相消求和了.化简时要注意观察已知条件，看到要联想到差角的正切公式，再化简.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在三棱锥A﹣BCD中，△ABC和△ABD都是以AB为斜边的直角三角形，AB⊥CD，AB＝10，CD＝6．

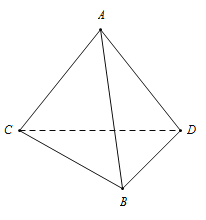
（1）问在AB上是否存在点E，使得AB⊥平面ECD？

（2）如果S△ABC＝S△ABD＝30，求二面角C﹣AB﹣D的大小．

（3）求三棱锥A﹣BCD体积的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】商店出售茶壶和茶杯，茶壶定价每个20元，茶杯每个5元，该商店推出两种优惠办法：（1）买一个茶壶赠一个茶杯；（２）按总价的９２％付款．

某顾客需购买茶壶４个，茶杯若干个（不少于４个），若购买茶杯数ｘ个，付款ｙ（元），分别建立两种优惠办法中ｙ与ｘ之间的函数关系式，并讨论该顾客买同样多的茶杯时，两种办法哪一种更优惠。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】抽样得到某次考试中高二年级某班名学生的数学成绩和物理成绩如下表：

学生编号
数学成绩
物里成绩

(1)在图中画出表中数据的散点图；

(2)建立关于的回归方程：(系数保留到小数点后两位).

(3)如果某学生的数学成绩为分，预测他本次的物理成绩(成绩取整数).

参考公式：回归方程为，其中，.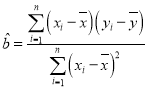

参考数据：，，.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】《中国青年报》2015年5月14日报道：“伴随着网络技术的蓬勃发展，国内电子商务获得了爆炸式的增长，2014年网上零售额达到了27898亿元，占社会消费品零售总额的10%，也就是说，人们日常消费中10%是通过网购，而且还以年30%，40%的速度增长."假设2014-2020年网上零售额每年的增长率均为35%，试算出2015-2020年每年的网上零售额（精确到1亿元）.