练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知数列
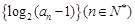
为等差数列,且
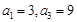
.
(1)求数列
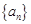
的通项公式;
(2)证明

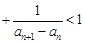
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知正项数列
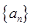
的前
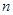
项和为
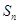
,且
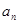
和
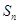
满足:
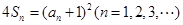
.
(1)求
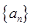
的通项公式;
(2)设
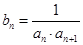
,求
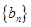
的前
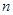
项和
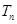
;
(3)在(2)的条件下,对任意
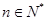
,
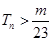
都成立,求整数
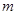
的最大值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知等差数列
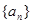
的公差不为零,其前n项和为
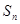
,若
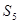
=70,且
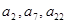
成等比数列,
(1)求数列
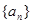
的通项公式;
(2)设数列
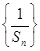
的前n项和为
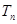
,求证:
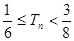
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知等差数列{
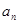
}的前n项和为Sn,公差d≠0,且S
3=9,a
1,a
3,a
7成等比数列.
(1)求数列{
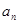
}的通项公式;
(2)设
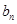
=
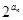
,求数列{
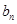
}的前n项和
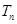
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知

是递增的等差数列,

,

为其前

项和,若

成等比数列,则

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知各项均为正数的等比数列{a
n}的公比为q,且0<q<
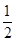
.
(1)在数列{a
n}中是否存在三项,使其成等差数列?说明理由;
(2)若a
1=1,且对任意正整数k,a
k-(a
k+1+a
k+2)仍是该数列中的某一项.
(ⅰ)求公比q;
(ⅱ)若b
n=-loga
n+1(
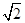
+1),S
n=b
1+b
2+…+b
n,T
r=S
1+S
2+…+S
n,试用S
2011表示T
2011.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等差数列
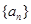
的前
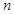
项和为
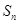
,若
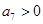
,
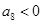
,则下列结论正确的是( )
查看答案和解析>>

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案 }的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.
}的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.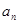 }的通项公式;
}的通项公式;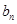 =
=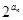 ,求数列{
,求数列{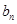 }的前n项和
}的前n项和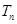 .
.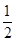 .
.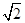 +1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.
+1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2011表示T2011.