
【题目】平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() :
:![]() 右焦点的直线
右焦点的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且椭圆
两点,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 为
为![]() 上的两点,若四边形
上的两点,若四边形![]() 的对角线
的对角线![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,函数的图象沿
,函数的图象沿![]() 轴向右平移
轴向右平移![]() 个单位长度后关于
个单位长度后关于![]() 轴对称,则下列结论正确的是______.(填序号)
轴对称,则下列结论正确的是______.(填序号)
①![]() 是函数
是函数![]() 图象的一个对称中心;
图象的一个对称中心;
②![]() 在区间
在区间![]() 上的最小值为-2;
上的最小值为-2;
③![]() 的单调递增区间是
的单调递增区间是![]() ;
;
④函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 时只有一个交点.
时只有一个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论:
(1)某学校从编号依次为001,002,…,900的900个学生中用系统抽样的方法抽取一个样本,已知样本中有两个相邻的编号分别为053,098,则样本中最大的编号为862.
(2)甲组数据的方差为5,乙组数据为5、6、9、10、5,那么这两组数据中较稳定的是甲.
(3)若两个变量的线性相关性越强,则相关系数![]() 的值越接近于1.
的值越接近于1.
(4)对A、B、C三种个体按3:1:2的比例进行分层抽样调查,若抽取的A种个体有15个,则样本容量为30.
则正确的个数是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 绕直线
绕直线![]() 翻转成
翻转成![]() (
(![]() 平面
平面![]() ),
),![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中,①与平面
翻折过程中,①与平面![]() 垂直的直线必与直线
垂直的直线必与直线![]() 垂直;②线段
垂直;②线段![]() 的长恒为
的长恒为![]() ③异面直线
③异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ④当三棱锥的体积最大时,三棱锥
④当三棱锥的体积最大时,三棱锥![]() 外接球的体积是
外接球的体积是![]() .上面说法正确的所有序号是( )
.上面说法正确的所有序号是( )
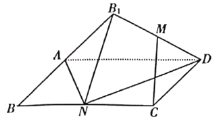
A.①②④B.①③④C.②③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎COVID-19疫情发生以来,在世界各地逐渐蔓延.在全国人民的共同努力和各级部门的严格管控下,我国的疫情已经得到了很好的控制.然而,每个国家在疫情发生初期,由于认识不足和措施不到位,感染确诊人数都会出现加速增长.如表是小王同学记录的某国从第一例新型冠状病毒感染确诊之日开始,连续8天每日新型冠状病毒感染确诊的累计人数.
日期代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
累计确诊人数 | 4 | 8 | 16 | 31 | 51 | 71 | 97 | 122 |
为了分析该国累计感染确诊人数的变化趋势,小王同学分别用两种模型:
①![]() ,②
,②![]() 对变量
对变量![]() 和
和![]() 的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差
的关系进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差![]() ,且经过计算得
,且经过计算得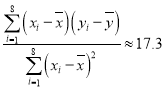 ,
,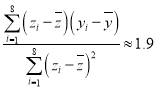 ,其中
,其中![]() ,
,![]() ,
,
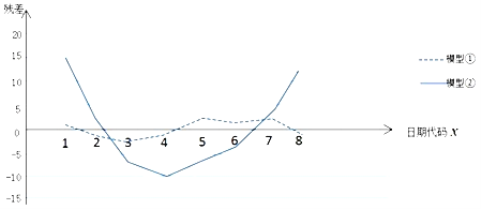
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由;
(2)根据(1)中选定的模型求出相应的回归方程;
(3)如果第9天该国仍未采取有效的防疫措施,试根据(2)中所求的回归方程估计该国第9天新型冠状病毒感染确诊的累计人数.(结果保留为整数)
附:回归直线的斜率和截距的最小二乘估计公式分别为: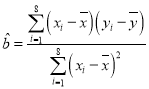 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度y(单位:cm)的情况如下表:
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2019年12月份AQI指数M的频数分布表如下:
M |
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,若x与y之间具有线性关系,试根据上述数据求出y关于x的线性回归方程;
,若x与y之间具有线性关系,试根据上述数据求出y关于x的线性回归方程;
(2)王先生在该市开了一家洗车店,洗车店每天的平均收入与AQI指数的相关关系如下表:
M |
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
估计王先生的洗车店2019年12月份每天的平均收入.
附参考公式:![]() ,其中
,其中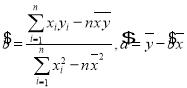
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ax2-(a2+b)x+aln x(a,b∈R).
ax2-(a2+b)x+aln x(a,b∈R).
(Ⅰ)当b=1时,求函数f(x)的单调区间;
(Ⅱ)当a=-1,b=0时,证明:f(x)+ex>-![]() x2-x+1(其中e为自然对数的底数)
x2-x+1(其中e为自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com