练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某学校高一、高二、高三年级的学生人数之比为3∶3∶4，现用分层抽样的方法从该校高中三个年级的学生中抽取一个容量为50的样本，则应从高二年级抽取名学生．

    【答案】15
    【解析】设应从高二年级抽取x名学生，则x∶50＝3∶10，解得x＝15.由分层抽样的特点可以得出答案.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】圆心在直线x﹣y+2=0上，且与两坐标轴都相切的圆的方程为（　　）

    A. （x+1）2+（y﹣1）2=1 B. （x﹣1）2+（y+1）2=1 C. （x﹣1）2+（y+1）2=2 D. （x﹣1）2+（y﹣1）2=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，（且）．

    （1）若，求函数在区间上的值域；

    （2）当时，函数在区间上的最小值大于在上的最小值，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从12件同类产品中(其中10件正品,2件次品),任意抽取6件产品,下列说法中正确的是(　　)

    A. 抽出的6件产品必有5件正品,1件次品

    B. 抽出的6件产品中可能有5件正品,1件次品

    C. 抽取6件产品时,逐个不放回地抽取,前5件是正品,第6件必是次品

    D. 抽取6件产品时,不可能抽得5件正品,1件次品

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司2016年前三个月的利润（单位：百万元）如下：

    月份

    1

    2

    3

    利润

    2

    3.9

    5.5

    （1）求利润关于月份的线性回归方程；

    （2）试用（1）中求得的回归方程预测4月和5月的利润；

    （3）试用（1）中求得的回归方程预测该公司2016年从几月份开始利润超过1000万？

    相关公式：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C:, 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线．

    （1）若抛物线C在点M的法线的斜率为，求点M的坐标；

    （2）设P为C对称轴上的一点，在C上是否存在点，使得C在该点的法线通过点P．若有，求出这些点，以及C在这些点的法线方程；若没有，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知随机变量ξ+η=8,若ξ～B(10,0.6),则E(η),D(η)分别是　(　　)

    A. 6和2.4 B. 2和2.4

    C. 2和5.6 D. 6和5.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司计划购买2台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：

    以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记表示2台机器三年内共需更换的易损零件数，表示购买2台机器的同时购买的易损零件数．

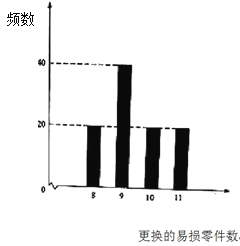
    （I）求的分布列；

    （II）若要求，确定的最小值；

    （III）以购买易损零件所需费用的期望值为决策依据，在与之中选其一，应选用哪个？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某服装厂生产一种服装，每件服装的成本为40元，出厂单价为60元，该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低0.02元，根据市场调查，销售商一次订购量不会超过500件.

    （1）设一次订购量为件，服装的实际出厂单价为元，写出函数的表达式；

    （2）当销售商一次订购多少件服装时，该服装厂获得的利润最大？并求出最大值.

    查看答案和解析>>

    同步练习册答案