
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f′′(x)是f′(x)的导数,若方程f′′(x)有实数解x0 , 则称点(x0 , f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数f(x)= ![]() x3﹣
x3﹣ ![]() x2+3x﹣
x2+3x﹣ ![]() ,请你根据这一发现,计算f(
,请你根据这一发现,计算f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业团队拟生产![]() 两种产品,根据市场预测,
两种产品,根据市场预测, ![]() 产品的利润与投资额成正比(如图1),
产品的利润与投资额成正比(如图1),![]() 产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)
产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)

(1)分別将![]() 两种产品的利润
两种产品的利润![]() 、
、![]() 表示为投资额
表示为投资额![]() 的函数;
的函数;
(2)该团队已筹集到10 万元资金,并打算全部投入![]() 两种产品的生产,问:当
两种产品的生产,问:当![]() 产品的投资额为多少万元时,生产
产品的投资额为多少万元时,生产![]() 两种产品能获得最大利润,最大利润为多少?
两种产品能获得最大利润,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={y|y=log2x,x≥4},B={y|y=( ![]() )x , ﹣1≤x≤0}.
)x , ﹣1≤x≤0}.
(1)求A∩B;
(2)若集合C={x|a≤x≤2a﹣1},且C∪B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
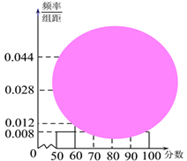
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图:
![]() 求分数在
求分数在![]() 的频率及全班人数;
的频率及全班人数;
![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)﹣ ![]() x.
x.
(1)试判断函数f(x)的奇偶性并证明;
(2)设g(x)=log4(a2x﹣ ![]() a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
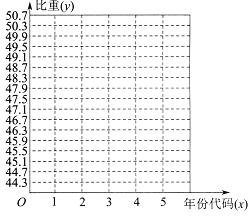
【题目】根据“2015年国民经济和社会发展统计公报” 中公布的数据,从2011 年到2015 年,我国的
第三产业在![]() 中的比重如下:
中的比重如下:
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
第三产业比重 |
|
|
|
|
|
(1)在所给坐标系中作出数据对应的散点图;
(2)建立第三产业在![]() 中的比重
中的比重![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在![]() 中的比重.
中的比重.
附注: 回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
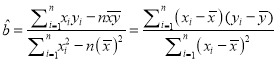 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足 ![]() ?
?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com