
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()
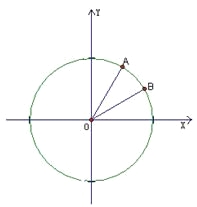
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】自2017年,大连“蜗享出行”正式引领共享汽车,改变人们传统的出行理念,给市民出行带来了诸多便利![]() 该公司购买了一批汽车投放到市场给市民使用
该公司购买了一批汽车投放到市场给市民使用![]() 据市场分析,每辆汽车的营运累计收入
据市场分析,每辆汽车的营运累计收入![]() 单位:元
单位:元![]() 与营运天数
与营运天数![]() 满足
满足![]() .
.
![]() 要使营运累计收入高于1400元求营运天数的取值范围;
要使营运累计收入高于1400元求营运天数的取值范围;
![]() 每辆汽车营运多少天时,才能使每天的平均营运收入最大?
每辆汽车营运多少天时,才能使每天的平均营运收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若中心在原点的椭圆![]() 与双曲线
与双曲线![]() 有共同的焦点,且它们的离心率互为倒数,圆
有共同的焦点,且它们的离心率互为倒数,圆![]() 的直径是椭圆
的直径是椭圆![]() 的长轴,C是椭圆的上顶点,动直线AB过C点且与圆
的长轴,C是椭圆的上顶点,动直线AB过C点且与圆![]() 交于A、B两点,CD垂直于AB交椭圆于点D.
交于A、B两点,CD垂直于AB交椭圆于点D.

(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积的最大值,并求此时直线AB的方程.
面积的最大值,并求此时直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴非负半轴建立平面直角坐标系.
轴非负半轴建立平面直角坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上一动点,过点
上一动点,过点![]() 作线段
作线段![]() 的垂线交曲线
的垂线交曲线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知相互啮合的两个齿轮,大轮有48齿,小轮有20齿,当大轮转动一周时,小轮转动的角是________度,即________rad.如果大轮的转速为![]() (转/分),小轮的半径为10.5cm,那么小轮周上一点每1s转过的弧长是________.
(转/分),小轮的半径为10.5cm,那么小轮周上一点每1s转过的弧长是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com