
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)设曲线![]() ,点
,点![]() ,
,![]() 为该曲线上不同的两点.求证:当
为该曲线上不同的两点.求证:当![]() 时,直线
时,直线![]() 的斜率大于-1.
的斜率大于-1.
【答案】(Ⅰ)当![]() 时,
时,![]() 的减区间是
的减区间是![]() ,无增区间;当
,无增区间;当![]() 时,
时,![]() 的减区间是
的减区间是![]() ,增区间是
,增区间是![]() .(Ⅱ)证明见解析.
.(Ⅱ)证明见解析.
【解析】
(Ⅰ)由![]() ,求导得
,求导得![]() ,
,
再分![]() 和
和![]() 两种情况分类讨论求解.
两种情况分类讨论求解.
(Ⅱ)由![]() ,得
,得![]() ,设
,设![]() ,要证直线
,要证直线![]() 的斜率大于-1.,只需证
的斜率大于-1.,只需证![]() ,只需证
,只需证![]() .即证
.即证![]() 在
在![]() 上是增函数即可.
上是增函数即可.
(Ⅰ)因为![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上是减函数,
上是减函数,
当![]() 时,令
时,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是减函数,
上是减函数,
综上:当![]() 时,
时,![]() 的减区间是
的减区间是![]() .
.
当![]() 时,
时,![]() 的减区间是
的减区间是![]() ,增区间是
,增区间是![]() .
.
(Ⅱ)因为![]() ,
,
所以![]() ,设
,设![]() ,
,
要证直线![]() 的斜率大于-1.,
的斜率大于-1.,
只需证![]() ,
,
只需证![]() ,
,
只需证![]() .
.
即证![]() 在
在![]() 上是增函数,
上是增函数,
要证![]() 在
在![]() 上是增函数,
上是增函数,
只需证当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
只需证当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
令![]()
所以当![]() 时,
时,![]() 在
在![]() 上恒成立
上恒成立
以上各步可逆
所以直线![]() 的斜率大于-1.
的斜率大于-1.


科目:高中数学 来源: 题型:
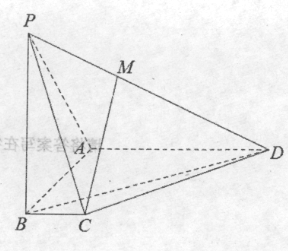
【题目】如图,在四棱锥![]() 中:
中:![]() 底面ABCD,底面ABCD为梯形,
底面ABCD,底面ABCD为梯形,![]() ,
,![]() ,且
,且![]() ,BC=1,M为棱PD上的点。
,BC=1,M为棱PD上的点。
(Ⅰ)若![]() ,求证:
,求证:![]() 平面PAB;
平面PAB;
(Ⅱ)求直线BD与平面PAD所成角的大小;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙、丙、丁、戊五名志愿者中选派三人分别从事翻译、导游、礼仪三项不同工作,若其中乙和丙只能从事前两项工作,其余三人均能从事这三项工作,则不同的选派方案共有( )
A.36种B.12种C.18种D.24种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年起,新高考科目设置采用“![]() ”模式,普通高中学生从高一升高二时将面临着选择物理还是历史的问题,某校抽取了部分男、女学生调查选科意向,制作出如右图等高条形图,现给出下列结论:
”模式,普通高中学生从高一升高二时将面临着选择物理还是历史的问题,某校抽取了部分男、女学生调查选科意向,制作出如右图等高条形图,现给出下列结论:
①样本中的女生更倾向于选历史;
②样本中的男生更倾向于选物理;
③样本中的男生和女生数量一样多;
④样本中意向物理的学生数量多于意向历史的学生数量.
根据两幅条形图的信息,可以判断上述结论正确的有( )


A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某地区随机抽测120名成年女子的血清总蛋白含量(单位:![]() ),由测量结果得如图频数分布表:
),由测量结果得如图频数分布表:
(1)①仔细观察表中数据,算出该样本平均数![]() ______;
______;
②由表格可以认为,该地区成年女子的血清总蛋白含量Z服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本标准差s.经计算,该样本标准差
近似为样本标准差s.经计算,该样本标准差![]() .
.
医学上,Z过高或过低都为异常,Z的正常值范围通常取关于![]() 对称的区间
对称的区间![]() ,且Z位于该区间的概率为
,且Z位于该区间的概率为![]() ,试用该样本估计该地区血清总蛋白正常值范围.
,试用该样本估计该地区血清总蛋白正常值范围.
120名成年女人的血清总蛋白含量的频数分布表 | |||
分组 | 频数f | 区间中点值x |
|
| 2 | 65 | 130 |
| 8 | 67 | 536 |
| 12 | 69 | 828 |
| 15 | 71 | 1065 |
| 25 | 73 | 1825 |
| 24 | 75 | 1800 |
| 16 | 77 | 1232 |
| 10 | 79 | 790 |
| 7 | 81 | 567 |
| 1 | 83 | 83 |
合计 | 120 | 8856 | |
(2)结合(1)中的正常值范围,若该地区有5名成年女子检测血清总蛋白含量,测得数据分别为83.2,80,73,59.5,77,从中随机抽取2名女子,设血清总蛋白含量不在正常值范围的人数为X,求X的分布列和数学期望.
附:若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,60件,30件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从乙车间的产品中抽取了2件。
(Ⅰ)应从甲、丙两个车间的产品中分别抽取多少件,样本容量n为多少?
(Ⅱ)设抽出的n件产品分别用![]() ,
,![]() ,…,
,…,![]() 表示,现从中随机抽取2件产品。
表示,现从中随机抽取2件产品。
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2件产品来自不同车间”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)如图(1)已知E,F,G,H为空间四边形ABCD的边AB,BC,CD,DA上的点,且EH![]() FG.求证:EH
FG.求证:EH![]() BD.
BD.
(2)如图(2):S是平行四边形ABCD平面外一点,M,N分别是SA,BD上的点,且![]() ,求证:MN
,求证:MN![]() 平面SBC.
平面SBC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com