
【题目】如图,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形, ![]() 平面
平面![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
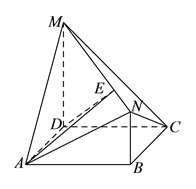
(I)求证: ![]() 平面
平面![]() .
.
(II)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(III)![]() 为直线
为直线![]() 上一点,且平面
上一点,且平面![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
【答案】(I)见解析;(II)![]() .
.
【解析】试题分析:(Ⅰ)通过证明平面与平面平行的判定定理证明平面AMD∥平面BCN,然后证明AM∥平面BCN;
(Ⅱ)以D为原点,DA,DC,DM所在直线分别为x,y,z轴,建立空间直角坐标系,求出平面MNC的法向量以及直线AN向量,然后求AN与平面MNC所成角的正弦值;
(Ⅲ)设E(x,y,z),![]() ,得到
,得到![]() 点的坐标为
点的坐标为![]() ,通过平面
,通过平面![]() 平面
平面![]() ,只要
,只要![]() ,
, ![]() 即可.
即可.
试题解析:
(I)证明:∵![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(也可建立直角坐标系,证明![]() 垂直平面
垂直平面![]() 的法向量,酌情给分)
的法向量,酌情给分)
(II)∵![]() 平面
平面![]() ,
, ![]() 是正方形,
是正方形,
所以,可选点![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() ,
, ![]() ,
, ![]() 轴,建立空间直角坐标系(如图),
轴,建立空间直角坐标系(如图),
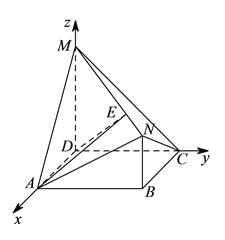
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则![]() ,令
,令![]() ,则
,则![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
∴![]() .
.
(III)设![]() ,
, ![]() ,
,
∴![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() .
.
∵![]() 面
面![]() ,
,
∴![]() ,欲使平面
,欲使平面![]() 平面
平面![]() ,只要
,只要![]() ,
,
∵![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
所以![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】《算法统综》是明朝程大位所著数学名著,其中有这样一段表述:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一”,其意大致为:有一七层宝塔,每层悬挂的红灯数为上一层的两倍,共有381盏灯,则塔从上至下的第三层有( )盏灯.
A.14
B.12
C.10
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②基本事件空间是Ω={1,2,3,4,5,6},若事件A={1,3},B={3,5,6},A,B为互斥事件,但不是对立事件;
③某校高三(1)班和高三(2)班的人数分别是m,n,若一模考试数学平均分分别是a,b,则这两个班的数学平均分为![]() ;
;
④如果平面外的一条直线上有两个点到这个平面的距离相等,那么这条直线与这个平面的位置关系为平行或相交。
其中真命题的序号是__________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从参加某次高中英语竞赛的学生中抽出100名,将其成绩整理后,绘制频率分布直方图(如图所示).其中样本数据分组区间为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
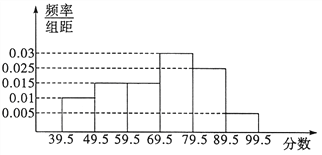
(Ⅰ)试求图中![]() 的值,并计算区间
的值,并计算区间![]() 上的样本数据的频率和频数;
上的样本数据的频率和频数;
(Ⅱ)试估计这次英语竞赛成绩的众数、中位数及平均成绩(结果精确到![]() ).
).
注:同一组数据用该组区间的中点值作为代表
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱台ABC﹣A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6 
(1)求证:BC1⊥平面AA1C1C
(2)点D是B1C1的中点,求二面角A1﹣BD﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:集合![]() ,其中
,其中
![]() .
.![]() ,称
,称![]() 为
为![]() 的第
的第![]() 个坐标分量.若
个坐标分量.若![]() ,且满足如下两条性质:
,且满足如下两条性质:
①![]() 中元素个数不少于
中元素个数不少于![]() 个.
个.
②![]() ,
,![]() ,
,![]() ,存在
,存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 的第
的第![]() 个坐标分量都是
个坐标分量都是![]() .则称
.则称![]() 为
为![]() 的一个好子集.
的一个好子集.
(![]() )若
)若![]() 为
为![]() 的一个好子集,且
的一个好子集,且![]() ,
,![]() ,写出
,写出![]() ,
,![]() .
.
(![]() )若
)若![]() 为
为![]() 的一个好子集,求证:
的一个好子集,求证:![]() 中元素个数不超过
中元素个数不超过![]() .
.
(![]() )若
)若![]() 为
为![]() 的一个好子集且
的一个好子集且![]() 中恰好有
中恰好有![]() 个元素,求证:一定存在唯一一个
个元素,求证:一定存在唯一一个![]() ,使得
,使得![]() 中所有元素的第
中所有元素的第![]() 个坐标分量都是
个坐标分量都是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com