分析:(1)求出f′(x),因为x1,x2是函数的两个极值点,所以x1,x2是f′(x)=0的两个实数根,根据a大于0,利用韦达定理得到两根之积小于0即两根异号,且表示出|x1|+|x2|,根据其值等于2列出a与b的关系式即可;
(2)从(1)中a与b的关系式中找出a的取值范围即为g(a)的定义域,求出g′(a)=0时a的值,利用a的值在定义域范围中,讨论g′(a)的符号得到g(a)的单调区间,利用g(a)的增减性即可得到g(a)的最值,即可得到g(a)的值域.
解答:解:(1)f′(x)=ax
2+bx-a
2∵x
1,x
2是函数f(x)的两个极值点,
∴x
1,x
2是方程f′(x)=ax
2+bx-a
2=0的两个实数根.
∵a>0,x
1x
2=-a<0,x
1+x
2=-
,
∴|x
1|+|x
2|=|x
1-x
2|=
=
∵|x
1|+|x
2|=2,
∴
=2即a与b的关系式为b
2-4a
2+4a
3=0;
(2)由(1)知b
2-4a
2+4a
3=0,即b
2=4a
2-4a
3≥0,∴0<a≤1
∴函数g(a)的定义域为(0,1]
g′(a)=a
2-
a+1=(a-
)(a-2)
∴a=
是函数g(a)的极值点
∴a,g′(a),g(a)的变化如下:
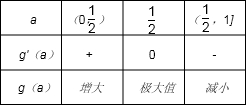
∴g(1)≤g(a)≤g(
)即
≤g(a)≤
∴g(a)的值域为[
,
]
点评:本题要求学生会利用导函数的正负得到函数的单调性,会根据函数的增减性得到函数的极值,灵活运用韦达定理化简求值,会求函数的定义域和值域,是一道中档题.



