
ЁОЬтФПЁПЖдгкдкЧјМф[mЃЌn]ЩЯгавтвхЕФСНИіКЏЪ§fЃЈxЃЉгыgЃЈxЃЉЃЌШчЙћЖдШЮвтxЁЪ[mЃЌn]Ољга|fЃЈxЃЉЉgЃЈxЃЉ|Ём1ЃЌдђГЦfЃЈxЃЉгыgЃЈxЃЉдк[mЃЌn]ЩЯЪЧНгНќЕФЃЛЗёдђГЦfЃЈxЃЉгыgЃЈxЃЉдк[mЃЌn]ЩЯЪЧЗЧНгНќЕФЃЎЯжгаСНИіКЏЪ§f1ЃЈxЃЉ=logaЃЈxЉ3aЃЉЃЌгыf2ЃЈxЃЉ=loga ![]() ЃЈaЃО0ЃЌaЁй1ЃЉЃЌИјЖЈЧјМф[a+2ЃЌa+3]ЃЎ
ЃЈaЃО0ЃЌaЁй1ЃЉЃЌИјЖЈЧјМф[a+2ЃЌa+3]ЃЎ
ЃЈ1ЃЉШєf1ЃЈxЃЉгыf1ЃЈxЃЉдкИјЖЈЧјМф[a+2ЃЌa+3]ЩЯЖМгавтвхЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЬжТлf1ЃЈxЃЉгыf1ЃЈxЃЉдкИјЖЈЧјМф[a+2ЃЌa+3]ЩЯЪЧЗёЪЧНгНќЕФЃП
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКвЊЪЙf1ЃЈxЃЉгыf2ЃЈxЃЉгавтвхЃЌдђга 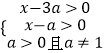 ЃЌ
ЃЌ
вЊЪЙf1ЃЈxЃЉгыf2ЃЈxЃЉдкИјЖЈЧјМф[a+2ЃЌa+3]ЩЯЖМгавтвхЃЌЕШМлгкЃК ![]() ЃЌЫљвд0ЃМaЃМ1
ЃЌЫљвд0ЃМaЃМ1
ЃЈ2ЃЉНтЃКf1ЃЈxЃЉгыf2ЃЈxЃЉдкИјЖЈЧјМф[a+2ЃЌa+3]ЩЯЪЧНгНќЕФЃЌ
|f1ЃЈxЃЉЉfЃЈx2ЃЉ|Ём1|logaЃЈxЉ3aЃЉЉ ![]() |Ём1|loga[ЃЈxЉ3aЃЉЃЈxЉaЃЉ]|Ём1aЁмЃЈxЉ2aЃЉ2Љa2
|Ём1|loga[ЃЈxЉ3aЃЉЃЈxЉaЃЉ]|Ём1aЁмЃЈxЉ2aЃЉ2Љa2 ![]() ЖдгкШЮвтxЁЪ[a+2ЃЌa+3]КуГЩСЂЃЎ
ЖдгкШЮвтxЁЪ[a+2ЃЌa+3]КуГЩСЂЃЎ
ЩшhЃЈxЃЉ=ЃЈxЉ2aЃЉ2Љa2ЃЌxЁЪ[a+2ЃЌa+3]ЃЌ
ЧвЦфЖдГЦжсx=2aЃМ2дкЧјМф[a+2ЃЌa+3]ЕФзѓБпЃЌ
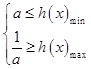
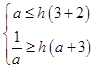
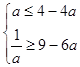
![]() ЃЌ
ЃЌ
ЫљвдЕБ ![]() ЃЌЪБЃЌf1ЃЈxЃЉгыf2ЃЈxЃЉдкИјЖЈЧјМф[a+2ЃЌa+3]ЩЯЪЧНгНќЕФ
ЃЌЪБЃЌf1ЃЈxЃЉгыf2ЃЈxЃЉдкИјЖЈЧјМф[a+2ЃЌa+3]ЩЯЪЧНгНќЕФ
ЁОНтЮіЁПЃЈ1ЃЉвЊЪЙf1ЃЈxЃЉгыf2ЃЈxЃЉгавтвхЃЌдђга 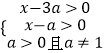 ЃЌМД
ЃЌМД ![]() ЃЌДгЖјЧѓГіaЕФШЁжЕЗЖЮЇЃЎЃЈ2ЃЉf1ЃЈxЃЉгыf2ЃЈxЃЉдкИјЖЈЧјМф[a+2ЃЌa+3]ЩЯЪЧНгНќЕФЃЌ
ЃЌДгЖјЧѓГіaЕФШЁжЕЗЖЮЇЃЎЃЈ2ЃЉf1ЃЈxЃЉгыf2ЃЈxЃЉдкИјЖЈЧјМф[a+2ЃЌa+3]ЩЯЪЧНгНќЕФЃЌ
|f1ЃЈxЃЉЉfЃЈx2ЃЉ|Ём1|logaЃЈxЉ3aЃЉЉ ![]() |Ём1|loga[ЃЈxЉ3aЃЉЃЈxЉaЃЉ]|Ём1aЁмЃЈxЉ2aЃЉ2Љa2
|Ём1|loga[ЃЈxЉ3aЃЉЃЈxЉaЃЉ]|Ём1aЁмЃЈxЉ2aЃЉ2Љa2 ![]() ЖдгкШЮвтxЁЪ[a+2ЃЌa+3]КуГЩСЂЃЎ
ЖдгкШЮвтxЁЪ[a+2ЃЌa+3]КуГЩСЂЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌФГЙЋТЗ![]() вЛВргавЛПщПеЕи
вЛВргавЛПщПеЕи![]() ЃЌЦфжа
ЃЌЦфжа ![]() ЃЌ
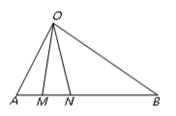
ЃЌ![]() ЃЎЕБЕиеўИЎФтдкжаМфПЊЭквЛИіШЫЙЄКўЁїOMNЃЌЦфжаMЃЌNЖМдкБпABЩЯЃЈMЃЌNВЛгыAЃЌBжиКЯЃЌMдкAЃЌNжЎМфЃЉЃЌЧвЁЯMONЃН30ЁуЃЎ
ЃЎЕБЕиеўИЎФтдкжаМфПЊЭквЛИіШЫЙЄКўЁїOMNЃЌЦфжаMЃЌNЖМдкБпABЩЯЃЈMЃЌNВЛгыAЃЌBжиКЯЃЌMдкAЃЌNжЎМфЃЉЃЌЧвЁЯMONЃН30ЁуЃЎ
ЃЈ1ЃЉШєMдкОрРыAЕу2 kmДІЃЌЧѓЕуMЃЌNжЎМфЕФОрРыЃЛ
ЃЈ2ЃЉЮЊНкЪЁЭЖШызЪН№ЃЌШЫЙЄКўЁїOMNЕФУцЛ§вЊОЁПЩФмаЁЃЎЪдШЗЖЈMЕФЮЛжУЃЌЪЙЁїOMNЕФУцЛ§зюаЁЃЌВЂЧѓГізюаЁУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊaЁЂbЁЪRЃЌЯђСП ![]() =ЃЈx ЃЌ 1ЃЉЃЌ
=ЃЈx ЃЌ 1ЃЉЃЌ ![]() =ЃЈЉ1ЃЌbЉxЃЉЃЌКЏЪ§fЃЈxЃЉ=aЉ
=ЃЈЉ1ЃЌbЉxЃЉЃЌКЏЪ§fЃЈxЃЉ=aЉ ![]() ЪЧХМКЏЪ§ЃЎ
ЪЧХМКЏЪ§ЃЎ
ЃЈ1ЃЉЧѓbЕФжЕЃЛ
ЃЈ2ЃЉШєдкКЏЪ§ЖЈвхгђФкзмДцдкЧјМф[mЃЌn]ЃЈmЃМnЃЉЃЌЪЙЕУy=fЃЈxЃЉдкЧјМф[mЃЌn]ЩЯЕФКЏЪ§жЕзщГЩЕФМЏКЯвВЪЧ[mЃЌn]ЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ![]() ,ОиаЮ
,ОиаЮ![]() жа,
жа, ![]() ,
, ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() БпЩЯЕФЕу,Чв
БпЩЯЕФЕу,Чв![]() ,НЋ
,НЋ![]() би
би![]() елЦ№жС
елЦ№жС![]() ЮЛжУ(ШчЭМ
ЮЛжУ(ШчЭМ![]() ЫљЪО),СЌНс
ЫљЪО),СЌНс![]() ,Цфжа
,Цфжа![]() .
.
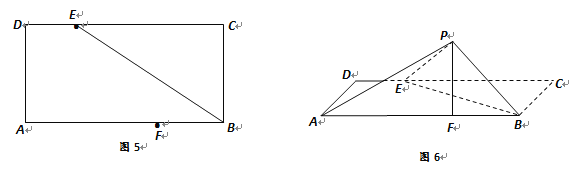
(Ђё) ЧѓжЄ: ![]() ЃЛ
ЃЛ
(Ђђ) дкЯпЖЮ![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЪЙЕУ
ЪЙЕУ![]() ?ШєДцдк,ЧѓГіЕу
?ШєДцдк,ЧѓГіЕу![]() ЕФЮЛжУЃЛШєВЛДцдк,ЧыЫЕУїРэгЩ.
ЕФЮЛжУЃЛШєВЛДцдк,ЧыЫЕУїРэгЩ.
(Ђѓ) ЧѓЕу![]() ЕН
ЕН![]() ЕФОрРы.
ЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊA={x| ![]() ЃМ3xЃМ9}ЃЌB={x|log2xЃО0}ЃЎ
ЃМ3xЃМ9}ЃЌB={x|log2xЃО0}ЃЎ
ЃЈ1ЃЉЧѓAЁЩBКЭAЁШBЃЛ
ЃЈ2ЃЉЖЈвхAЉB={x|xЁЪAЧвxB}ЃЌЧѓAЉBКЭBЉAЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПCPI ЪЧОгУёЯћЗбМлИёжИЪ§(consumer price index)ЕФМђГЦ.ОгУёЯћЗбМлИёжИЪ§ЃЌЪЧвЛИіЗДгГОгУёМвЭЅвЛАуЫљЙКТђЕФЯћЗбЦЗМлИёЫЎЦНБфЖЏЧщПіЕФКъЙлОМУжИБъ.ЯТУцЪЧИљОнЭГМЦОжЗЂВМЕФ2017Фъ1дТвЛ7дТЕФCPI ЭЌБШдіГЄгыЛЗБШдіГЄеЧЕјЗљЪ§ОнЛцжЦЕФелЯпЭМ.(зЂ:2017 Фъ2дТгы2016Фъ2дТЯрБШНЯЃЌНаЭЌБШЃЛ2017 Фъ2 дТгы2017 Фъ1дТЯрБШНЯЃЌНаЛЗБШ)ИљОнИУелЯпЭМЃЌдђЯТСаНсТлДэЮѓЕФЪЧЃЈ ЃЉ
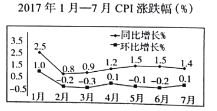
A. 2017 Фъ1дТвЛ7дТЗжБ№гы2016Фъ1дТвЛ7дТЯрБШНЯЃЌCPI гаеЧгаЕј
B. 2017 Фъ1дТвЛ7дТCPI гаеЧгаЕј
C. 2017Фъ1дТвЛ7дТЗжБ№гы2016Фъ1дТвЛ7дТЯрБШНЯЃЌ1дТCPI еЧЗљзюДѓ
D. 2017 Фъ2 дТвЛ7дТCPI еЧЕјВЈЖЏВЛДѓЃЌБфЛЏБШНЯЦНЮШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЗжБ№ЪЧЭждВ
ЗжБ№ЪЧЭждВ![]() ЕФзѓЁЂгвНЙЕуЃЌЖЏЕу
ЕФзѓЁЂгвНЙЕуЃЌЖЏЕу![]() дк
дк![]() ЩЯЃЌСЌНс
ЩЯЃЌСЌНс![]() ВЂбгГЄ
ВЂбгГЄ![]() жС
жС![]() ЕуЃЌЪЙЕУ
ЕуЃЌЪЙЕУ![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФЙьМЃЮЊ
ЕФЙьМЃЮЊ![]() .
.
(1)Чѓ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
(2)Щш![]() ЮЊзјБъдЕуЃЌЕу
ЮЊзјБъдЕуЃЌЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() НЛ
НЛ![]() гк
гк![]() ЕуЃЌШєжБЯп
ЕуЃЌШєжБЯп![]() ЕФаБТЪгыжБЯп
ЕФаБТЪгыжБЯп![]() ЕФаБТЪДцдкЧвВЛЮЊСуЃЌжЄУї: етСНЬѕжБЯпЕФаБТЪжЎБШЮЊЖЈжЕ.
ЕФаБТЪДцдкЧвВЛЮЊСуЃЌжЄУї: етСНЬѕжБЯпЕФаБТЪжЎБШЮЊЖЈжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЧњЯпyЃНx3ЃЋxЃ2дкЕуP0ДІЕФЧаЯпl1ЦНаагкжБЯп4xЃyЃ1ЃН0ЃЌЧвЕуP0дкЕкШ§ЯѓЯоЃЎ
(1)ЧѓP0ЕФзјБъЃЛ(2)ШєжБЯпlЁЭl1ЃЌЧвlвВЙ§ЧаЕуP0ЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЧв
ЃЌЧв![]() .
.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФМЋжЕЃЛ
ЕФМЋжЕЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌжЄУїЃК
ЪБЃЌжЄУїЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com