
【题目】![]() 个孩子在黄老师的后院玩球,突然传来一阵打碎玻璃的响声,黄老师跑去察看,发现一扇窗户玻璃被打破了,老师问:“谁打破的?”宝宝说:“是可可打破的.”可可说:“是毛毛打破的.”毛毛说:“可可说谎.”多多说:“我没有打破窗子.”如果只有一个小孩说的是实话,那么打碎玻璃的是( )
个孩子在黄老师的后院玩球,突然传来一阵打碎玻璃的响声,黄老师跑去察看,发现一扇窗户玻璃被打破了,老师问:“谁打破的?”宝宝说:“是可可打破的.”可可说:“是毛毛打破的.”毛毛说:“可可说谎.”多多说:“我没有打破窗子.”如果只有一个小孩说的是实话,那么打碎玻璃的是( )
A.宝宝B.可可C.多多D.毛毛
【答案】C
【解析】
根据题意,分别假设四个人打碎玻璃,结合他们的对话,得矛盾,即可得解.
假设是宝宝打碎玻璃,则宝宝说谎话,可可说谎话,毛毛说实话,多多说实话,与题意只有一个小孩说实话矛盾,所以假设不成立,即宝宝没有打碎玻璃;
假设是可可打碎玻璃,则宝宝说实话,可可说谎话,毛毛说实话,多多说实话,与题意只有一个小孩说实话矛盾,所以假设不成立,即可可没有打碎玻璃;
假设是多多打碎玻璃,则宝宝说谎话,可可说谎话,毛毛说实话,多多说谎话,与题意只有一个小孩说实话相符,所以假设成立,即多多打碎玻璃;
假设是毛毛打碎玻璃,则宝宝说谎话,可可说实话,毛毛说谎话,多多说实话,与题意只有一个小孩说实话矛盾,所以假设不成立,即毛毛没有打碎玻璃;
综上可知,是多多打碎玻璃
故选:C


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】下面是甲、乙两位同学高三上学期的5次联考数学成绩,现在只知其从第1次到第5次分数所在区间段分布的条形图(从左至右依次为第1至第5次),则从图中可以读出一定正确的信息是( )
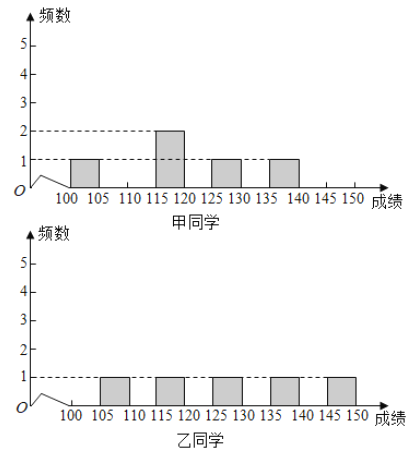
A.甲同学的成绩的平均数大于乙同学的成绩的平均数
B.甲同学的成绩的方差大于乙同学的成绩的方差
C.甲同学的成绩的极差小于乙同学的成绩的极差
D.甲同学的成绩的中位数小于乙同学的成绩的中位数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校科技节需要同学设计一幅矩形纸板宣传画,要求画面的面积为![]() (如图中的阴影部分),画面的上、下各留
(如图中的阴影部分),画面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.
空白.
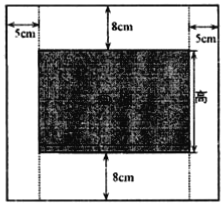
(1)如何设计画面的高与宽的尺寸,才能使整个宣传画所用纸张面积最小?
(2)如果按照第一问这样制作整个宣传画,在科技节结束以后,这整个宣传画纸板可再次作为某实验道具,并要求从整个宣传画板的四个角各截取一个相同的小正方形,做成一个长方体形的无盖容器.问截下的小正方形的边长(也就是该容器的高)是多少时,该容器的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车的购车费用是10万元,每年使用的保险费、养路费、汽油费约为![]() 万元,年维修费用第一年是
万元,年维修费用第一年是![]() 万元,第二年是
万元,第二年是![]() 万元,第三年是
万元,第三年是![]() 万元,…,以后逐年递增
万元,…,以后逐年递增![]() 万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用
万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用![]() 年的维修费用的和为
年的维修费用的和为![]() ,年平均费用为
,年平均费用为![]() .
.
(1)求出函数![]() ,
,![]() 的解析式;
的解析式;
(2)这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1) 解不等式![]() ;
;
(2) 设函数![]() ,若函数
,若函数![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(3) 当![]() 时,是否存在实数
时,是否存在实数![]() (其中
(其中![]() ),使得不等式
),使得不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年我国将加快阶梯水价推行,原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变.为响应国家政策,制定合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,抽取的数据的茎叶图如下(单位:吨):
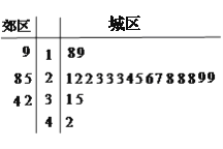
(1)在郊区的这5户居民中随机抽取2户,求其年人均用水量都不超过30吨的概率;
(2)设该城市郊区和城区的居民户数比为![]() ,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一梯次的居民用户用水价格保持不变.试根据样本估计总体的思想,分析此方案是否符合国家“保基本”政策.
,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一梯次的居民用户用水价格保持不变.试根据样本估计总体的思想,分析此方案是否符合国家“保基本”政策.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,与抛物线的准线相交于点
两点,与抛物线的准线相交于点![]() ,
, ![]() ,则
,则![]() 与
与![]() 的面积之比
的面积之比![]() __________.
__________.
【答案】![]()
【解析】
由题意可得抛物线的焦点![]() 的坐标为
的坐标为![]() ,准线方程为
,准线方程为![]() 。
。
如图,设![]() ,过A,B分别向抛物线的准线作垂线,垂足分别为E,N,则
,过A,B分别向抛物线的准线作垂线,垂足分别为E,N,则
![]() ,解得
,解得![]() 。
。
把![]() 代入抛物线
代入抛物线![]() ,解得
,解得![]() 。
。
∴直线AB经过点![]() 与点
与点![]() ,
,
故直线AB的方程为![]() ,代入抛物线方程解得
,代入抛物线方程解得![]() 。
。
∴![]() 。
。
在![]() 中,
中, ![]() ,
,
∴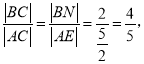
∴![]() 。答案:
。答案: ![]()
点睛:
在解决与抛物线有关的问题时,要注意抛物线的定义在解题中的应用。抛物线定义有两种用途:一是当已知曲线是抛物线时,抛物线上的点M满足定义,它到准线的距离为d,则|MF|=d,可解决有关距离、最值、弦长等问题;二是利用动点满足的几何条件符合抛物线的定义,从而得到动点的轨迹是抛物线.
【题型】填空题
【结束】
17
【题目】已知![]() 三个内角
三个内角![]() 所对的边分别是
所对的边分别是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圆半径为2,求
的外接圆半径为2,求![]() 周长的最大值.
周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com