
【题目】为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品,已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:![]() ,且每处理一顿二氧化碳得到可利用的化工产品价值为100元.
,且每处理一顿二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该单位不亏损?
【答案】(1)该单位每月处理量为400吨时,才能使每吨的平均处理成本最低(2)该单位不获利,需要国家每月至少补贴40000元,才能不亏损
【解析】
试题分析:(1)由题意可知,二氧化碳的每吨平均处理成本为:
![]() ,利用基本不等式,可得
,利用基本不等式,可得![]() 时,才能使每吨的平均处理恒本最低,最低成本为200元.(2)设该单位每月获利为
时,才能使每吨的平均处理恒本最低,最低成本为200元.(2)设该单位每月获利为![]() ,则
,则![]()
![]() ,利用二次函数的性质
,利用二次函数的性质
可得当![]() 时,
时,![]() 有最大值
有最大值![]() .故该单位不获利,需要国家每月至少补贴40000元,才能不亏损.
.故该单位不获利,需要国家每月至少补贴40000元,才能不亏损.
试题解析:(1)由题意可知,二氧化碳的每吨平均处理成本为:
![]() ,
,
当且仅当![]() ,即
,即![]() 时,才能使每吨的平均处理恒本最低,最低成本为200元.
时,才能使每吨的平均处理恒本最低,最低成本为200元.
(2)设该单位每月获利为![]() ,则
,则![]()
![]()
![]()
![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
故该单位不获利,需要国家每月至少补贴40000元,才能不亏损.


科目:高中数学 来源: 题型:
【题目】太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美,定义:能够将圆![]() 的周长和面积同时等分成两个部分的函数称为圆
的周长和面积同时等分成两个部分的函数称为圆![]() 的一个“太极函数”,则下列有关说法中:
的一个“太极函数”,则下列有关说法中:

①对于圆![]() 的所有非常数函数的太极函数中,一定不能为偶函数;
的所有非常数函数的太极函数中,一定不能为偶函数;
②函数![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
③存在圆![]() ,使得
,使得![]() 是圆
是圆![]() 的一个太极函数;
的一个太极函数;
④直线![]() 所对应的函数一定是圆
所对应的函数一定是圆![]() 的太极函数;
的太极函数;
⑤若函数![]() 是圆
是圆![]() 的太极函数,则
的太极函数,则![]()
所有正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).![]()
![]() .
.

(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾, 5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,并作出如下频率分布直方图(图1):
五组,并作出如下频率分布直方图(图1):
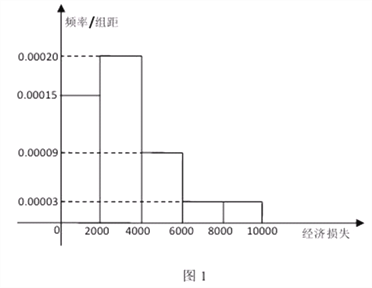
(1)试根据频率分布直方图估计小区平均每户居民的平均损失;
(同一组中的数据用该组区间的中点值作代表);
(2)小明向班级同学发出倡议,为该小区居民捐款,现从损失超过6000元的居民中随机
抽出2户进行捐款援助,求抽出的2户居民损失均超过8000元的概率;
(3)台风后区委会号召该小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,
在图2表格空白外填写正确数字,并说明是否有95%以上的把握认为捐款数额超过或
不超过500元和自身经济损失是否超过4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 | 30 | ||
捐款不超过500元 | 6 | ||
合计 |
附:临界值参考公式: 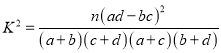 ,
, ![]() .
.
| 0.15 | 0.10 | 0.05 /td> | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数,给出下列命题:
①若函数f(x)是R上周期为3的偶函数,且满足f(1)=1,则f(2)-f(-4)=0;
②若函数f(x)满足f(x+1)f(x)=2 017,则f(x)是周期函数;
③若函数g(x)=![]() 是偶函数,则f(x)=x+1;
是偶函数,则f(x)=x+1;
④函数y=![]() 的定义域为
的定义域为![]() .
.
其中正确的命题是________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十八届五种全会公报指出:努力促进人口均衡发展,坚持计划生育的基本国策,完善人口发展战略,全面实施一对夫妇可生育两个孩子的政策,提高生殖保健、妇幼保健、托儿等公共服务水平.为了解适龄公务员对放开生育二胎政策的态度,某部门随机调查了100位30到40岁的公务员,得到情况如下表:
男公务员 | 女公务员 | |
生二胎 | 40 | 20 |
不生二胎 | 20 | 20 |
(1)是否有95%以上的把握认为“生二胎与性别有关”,并说明理由;
(2)把以上频率当概率,若从社会上随机抽取3位30到40岁的男公务员,记其中生二胎的人数为![]() ,求随机变量
,求随机变量![]() 的分布列,数学期望.
的分布列,数学期望.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 所在的平面与圆
所在的平面与圆![]() 所以的平面互相垂直,已知
所以的平面互相垂直,已知![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 的长为何值时,平面
的长为何值时,平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ?
?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com