
| A. | 8 | B. | 18 | C. | $\sqrt{13}$ | D. | 2$\sqrt{13}$ |
分析 画出图形,平行四边形的面积转化为4个三角形的面积,求出一个三角形的面积,乘以4得答案.
解答 解:如图,$\overrightarrow{AC}$=(-3,4),$\overrightarrow{BD}$=(3,2),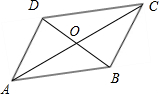
则$cos∠DOC=\frac{\overrightarrow{AC}•\overrightarrow{BD}}{|\overrightarrow{AC}|•|\overrightarrow{BD}|}$=$\frac{-1}{5\sqrt{13}}=-\frac{\sqrt{13}}{65}$,
∴$sin∠DOC=\sqrt{1-\frac{13}{6{5}^{2}}}=\frac{18\sqrt{13}}{65}$.
∴${S}_{四边形ABCD}=4×\frac{1}{2}|\overrightarrow{AC}|•|\overrightarrow{BD}|sin∠DOC$=$4×\frac{1}{2}×5×\sqrt{13}×\frac{18\sqrt{13}}{65}$=18.
故选:B.
点评 本题考查平面向量的数量积运算,考查了由数量积求两向量的夹角,训练了三角形面积的求法,是中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=xsinx | B. | y=$\frac{{e}^{x}+{e}^{-x}}{2}$ | C. | y=xlnx | D. | y=x3-2sinx+tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a≤1 | B. | a≤1 | C. | -1<a≤3 | D. | a<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com