
【题目】在![]() 中,内角
中,内角![]() 的对边分别为
的对边分别为![]() ,已知
,已知![]() .
.
![]() 求
求![]() ;
;
![]() 若
若![]() ,且
,且![]() 面积
面积![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由正弦定理,三角函数恒等变换的应用化简已知等式可得tanA=![]() ,结合范围A∈(0,π),可求A的值.
,结合范围A∈(0,π),可求A的值.
(2)由已知利用三角形的面积公式可求c的值,进而可求b的值,根据余弦定理可得a的值.
(1)∵![]() ,
,
∴b=2a(cosCcos![]() +sinCsin
+sinCsin![]() ),可得:b=acosC+
),可得:b=acosC+![]() asinC,
asinC,
由正弦定理可得:sinB=sinAcosC+![]() sinAsinC,
sinAsinC,
可得:sin(A+C)=sinAcosC+cosAsinC=sinAcosC+![]() sinAsinC,
sinAsinC,
可得:cosA=![]() sinA,可得:tanA=
sinA,可得:tanA=![]() ,
,
∵A∈(0,π),
∴A=![]()
(2)∵![]() ,且△ABC面积
,且△ABC面积![]() =
=![]() bcsinA=
bcsinA=![]() 2
2![]() c×c×
c×c×![]() ,
,
∴解得:c=2,b=4![]() ,
,
∴由余弦定理可得:a2=b2+c2-2bccosA=48+4-2×![]() ×2×
×2×![]() =28,解得:a=2
=28,解得:a=2![]()


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】某老师是省级课题组的成员,主要研究课堂教学目标达成度,为方便研究,从实验班中随机抽取30次的随堂测试成绩进行数据分析![]() 已知学生甲的30次随堂测试成绩如下
已知学生甲的30次随堂测试成绩如下![]() 满分为100分
满分为100分![]() :
:
88 58 50 36 75 39 57 62 72 51
85 39 57 53 72 46 64 74 53 50
44 83 70 63 71 64 54 62 61 42
![]() 把学生甲的成绩按
把学生甲的成绩按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,列出频率分布表,并画出频率分布直方图;
分成6组,列出频率分布表,并画出频率分布直方图;
![]() 为更好的分析学生甲存在的问题,从随堂测试成绩50分以下
为更好的分析学生甲存在的问题,从随堂测试成绩50分以下![]() 不包括50分
不包括50分![]() 的试卷中随机抽取3份进行分析,求恰有2份成绩在
的试卷中随机抽取3份进行分析,求恰有2份成绩在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地区2012年至2018年生活垃圾无害化处理量(单位:万吨)的折线图.
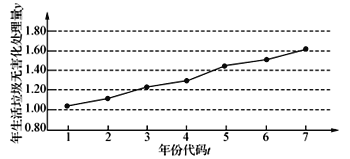
注:年份代码![]() 分别表示对应年份
分别表示对应年份![]() .
.
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() (
(![]() 线性相关较强)加以说明;
线性相关较强)加以说明;
(2)建立![]() 与
与![]() 的回归方程(系数精确到0.01),预测2019年该区生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2019年该区生活垃圾无害化处理量.
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(参考公式)相关系数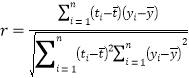 ,在回归方程
,在回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: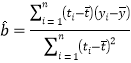 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中真命题的序号是( ).
①平面内到两定点距离之比等于常数![]() 的点的轨迹是圆;
的点的轨迹是圆;
②平面内与定点A(-3,0)和B(3,0)的距离之差等于4的点的轨迹为![]() ;
;
③点P是抛物线![]() 上的动点,点P在x轴上的射影是M,点A的坐标是
上的动点,点P在x轴上的射影是M,点A的坐标是![]() ,则
,则![]() 的最小值是
的最小值是![]() ;
;
④已知P为抛物线![]() 上一个动点,Q为圆
上一个动点,Q为圆![]() 上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是
上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是![]()
A.①B.②C.③D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为双曲线
为双曲线![]() :
: ![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线C于点
轴上方交双曲线C于点![]() ,且
,且![]()
(1)求双曲线C的方程;
(2)若直线![]() 与双曲线C恒有两个不同交点P和Q且
与双曲线C恒有两个不同交点P和Q且![]() (其中O为原点),求k的取值范围;
(其中O为原点),求k的取值范围;
(3)过双曲线C上任意一点R作该双曲线两条渐近线的垂线,垂足分别为M,N,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题![]() :方程
:方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线:命题
轴上的双曲线:命题![]() :若存在
:若存在![]() ,使得
,使得![]() 成立.
成立.
(1)如果命题![]() 是真命题,求实数
是真命题,求实数![]() 的取值范围;
的取值范围;
(2)如果“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源租赁汽车”.每次租车收费的标准由两部分组成:①里程计费:1元/公里;②时间计费:![]() 元/分.已知陈先生的家离上班公司
元/分.已知陈先生的家离上班公司![]() 公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为
公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为![]() (分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示
(分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示

将各时间段发生的频率视为概率,一次路上开车所用的时间视为用车时间,范围为![]()
![]() 分.
分.
(1)估计陈先生一次租用新能源租赁汽车所用的时间不低于![]() 分钟的概率;
分钟的概率;
(2)若公司每月发放![]() 元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按
元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按![]() 天计算),并说明理由.(同一时段,用该区间的中点值作代表)
天计算),并说明理由.(同一时段,用该区间的中点值作代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com