
���� ��1������ɵ�f��x��=2sin��2��x-$\frac{��}{6}$���������Ǻ����ĶԳ��Ժͦءʣ�-$\frac{1}{2}��\frac{5}{2}$���ɵæ�=1���ɵý���ʽ��
��2����������sinB=$\frac{\sqrt{5}}{3}$��cosB=$\frac{2}{3}$�������Ҷ����ͻ�������ʽ�ɵ�ac��3�������ɵá�ABC���S=$\frac{1}{2}$acsinB=$\frac{\sqrt{5}}{6}$ac��$\frac{\sqrt{5}}{2}$���ɵô𰸣�
��� �⣺��1������ɵ�f��x��=$\sqrt{3}$sin2��x-cos2��x=2sin��2��x-$\frac{��}{6}$����
�ߺ���f��x����ͼ�����ֱ��x=$\frac{��}{3}$�Գ�
��2�ء�$\frac{��}{3}$-$\frac{��}{6}$=k��+$\frac{��}{2}$�����=$\frac{3}{2}$k+1��k��Z
�ɦءʣ�-$\frac{1}{2}��\frac{5}{2}$���ɵæ�=1��
�ຯ��f��x���Ľ���ʽΪf��x��=2sin��2x-$\frac{��}{6}$����
��2�����ڡ�ABC�����B����f��$\frac{B}{2}+\frac{��}{12}$��=2sinB=$\frac{2\sqrt{5}}{3}$��
��sinB=$\frac{\sqrt{5}}{3}$��cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{2}{3}$����b=$\sqrt{2}$��
�������Ҷ����ɵ�2=a2+c2-2ac��$\frac{2}{3}$��2ac-$\frac{4}{3}$ac=$\frac{2}{3}$ac��
��ac��3�����ABC���S=$\frac{1}{2}$acsinB=$\frac{\sqrt{5}}{6}$ac��$\frac{\sqrt{5}}{2}$��
���ABC��������ֵΪ$\frac{\sqrt{5}}{2}$��
���� ���⿼�����Ǻ�ȱ任���漰���Ǻ����ĶԳ��Ժ����Ҷ����Լ������ε������ʽ�����е��⣮


 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
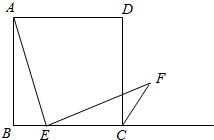 ��ͼ����֪�߳�Ϊ4��������ABCD��E��BC����һ���㣨��B��C���غϣ�������AE����EF��AE����BCD�����ƽ������F��BE=x����f��x��=$\overrightarrow{EC}$•$\overrightarrow{CF}$������f��x����ֵ���ǣ�0��4]������ECF������ʱ��|$\overrightarrow{EF}$|=2$\sqrt{5}$��
��ͼ����֪�߳�Ϊ4��������ABCD��E��BC����һ���㣨��B��C���غϣ�������AE����EF��AE����BCD�����ƽ������F��BE=x����f��x��=$\overrightarrow{EC}$•$\overrightarrow{CF}$������f��x����ֵ���ǣ�0��4]������ECF������ʱ��|$\overrightarrow{EF}$|=2$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-|x| | B�� | y=$\frac{1}{x}$ | C�� | y=3-x | D�� | y=2x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
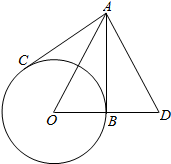 ��ͼ��AB��ACΪ��O�����ߣ�B��C���е㣬�ӳ�OB��D��ʹBD=OB������AD�������DAC=78�㣬��ô��ADO���ڣ�������
��ͼ��AB��ACΪ��O�����ߣ�B��C���е㣬�ӳ�OB��D��ʹBD=OB������AD�������DAC=78�㣬��ô��ADO���ڣ�������| A�� | 70�� | B�� | 64�� | C�� | 62�� | D�� | 51�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
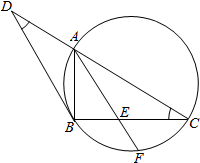 ��ͼ��BD�ǡ�ABC���Բ�����ߣ���A��BD��ƽ���߽�BC��E������ABC�����Բ��F��
��ͼ��BD�ǡ�ABC���Բ�����ߣ���A��BD��ƽ���߽�BC��E������ABC�����Բ��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
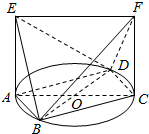 ��ͼ����֪AC��BDΪԲO����������ֱ����ֱ��AE��CF��ԲO����ƽ����������ߣ����߶�AE=CF=$\sqrt{2}$��AC=2��
��ͼ����֪AC��BDΪԲO����������ֱ����ֱ��AE��CF��ԲO����ƽ����������ߣ����߶�AE=CF=$\sqrt{2}$��AC=2���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com