练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知一个三角形的两内角分别为45°和60°，如果45°角所对的边长是6，那么60°角所对的边长为

    [　　]
    A．

    3

    B．

    3

    C．

    3

    D．

    2

    答案：A
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    15、给出命题：
    （1）在空间里，垂直于同一平面的两个平面平行；
    （2）设l，m是不同的直线，α是一个平面，若l⊥α，l∥m，则m⊥α；
    （3）已知α，β表示两个不同平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的充要条件；
    （4）若点P到三角形三个顶点的距离相等，则点P在该三角形所在平面内的射影是该三角形的外心；
    （5）a，b是两条异面直线，P为空间一点，过P总可以作一个平面与a，b之一垂直，与另一个平行．
    其中正确的命题是
    （2）（4）
    （只填序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面给出的几个命题中：
    ①若平面α∥平面β，AB，CD是夹在α，β间的线段，若AB∥CD，则AB=CD；
    ②a，b是异面直线，b，c是异面直线，则a，c一定是异面直线；
    ③过空间任一点，可以做两条直线和已知平面α垂直；
    ④平面α∥平面β，P∈α，PQ∥β，则PQ?α；
    ⑤若点P到三角形三个顶点的距离相等，则点P在该三角形所在平面内的射影是该三角形的外心；
    ⑥a，b是两条异面直线，P为空间一点，过P总可以作一个平面与a，b之一垂直，与另一个平行．
    其中正确的命题是
    ①④⑤
    ①④⑤
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知△ABC和△DBC是两个有公共斜边的直角三角形，并且AB=AD=AC=2a，CD=
    		6
    a    ．
    （1）若P是AC边上的一点，当△PDB的面积最小时，求二面角B-PD-C的正切值；
    （2）在（1）的条件下，求点C到平面PBD的距离；
    （3）能否找到一个球，使A，B，C，D都在该球面上，若不能，请说明理由；若能，求该球的内接正三棱柱的侧面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山西省康杰中学高二第一次月考文科数学试卷（带解析） 题型：填空题

    下面给出的几个命题中：
    ①若平面//平面，是夹在间的线段，若//，则；
    ②是异面直线，是异面直线，则一定是异面直线；
    ③过空间任一点，可以做两条直线和已知平面垂直；
    ④平面//平面，，//，则；
    ⑤若点到三角形三个顶点的距离相等，则点在该三角形所在平面内的射影是该三角形的外心；
    ⑥是两条异面直线，为空间一点, 过总可以作一个平面与之一垂直，与另一个平行.
    其中正确的命题是               .

    查看答案和解析>>

    科目：高中数学 来源：2014届山西省高二第一次月考文科数学试卷（解析版） 题型：填空题

    下面给出的几个命题中：

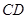    ①若平面//平面，是夹在间的线段，若//，则；

    ②是异面直线，是异面直线，则一定是异面直线；

    ③过空间任一点，可以做两条直线和已知平面垂直；

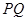    ④平面//平面，，//，则；

    ⑤若点到三角形三个顶点的距离相等，则点在该三角形所在平面内的射影是该三角形的外心；

    ⑥是两条异面直线，为空间一点, 过总可以作一个平面与之一垂直，与另一个平行.

    其中正确的命题是                .

     

    查看答案和解析>>

    同步练习册答案