
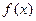 =
=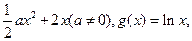
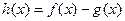 存在单调增区间,求
存在单调增区间,求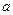 的取值范围;
的取值范围;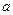 >0,使得方程
>0,使得方程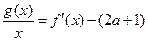 在区间
在区间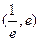 内有且只有两个不相等的实数根?若存在,求出
内有且只有两个不相等的实数根?若存在,求出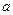 的取值范围?若不存在,请说明理由.
的取值范围?若不存在,请说明理由.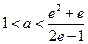 , 所以a的取值范围是(1,
, 所以a的取值范围是(1, 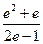 )
)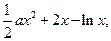 且x>0, …………………...1f
且x>0, …………………...1f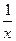 =
= ,…………………………………………………2f
,…………………………………………………2f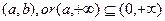 ……………………….……3f
……………………….……3f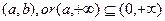 ……………………..……4f
……………………..……4f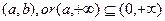 ……………………….……4f
……………………….……4f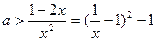 有解……………………………………………………….5f
有解……………………………………………………….5f 的最小值为
的最小值为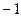 ……………………………………..……6f
……………………………………..……6f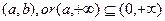 ……………………..……4f
……………………..……4f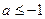 ,
, 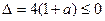 ,ax2+2x-1>0没有符合条解………………………5f
,ax2+2x-1>0没有符合条解………………………5f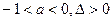 ,方程
,方程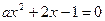 的两根是
的两根是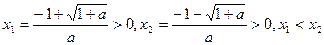 ,此时,区间
,此时,区间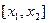 是所求的增区间。.
是所求的增区间。.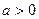 ,方程
,方程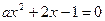 的两根是,
的两根是,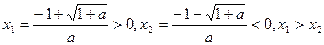 ,区间
,区间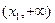 为所求的增区
为所求的增区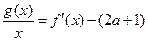
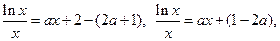
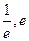 )内根的问题, 转化为函数H(x)在区间(
)内根的问题, 转化为函数H(x)在区间(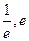 )内的零点问题………………………………………………………………….... 9f
)内的零点问题………………………………………………………………….... 9f 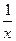 =
=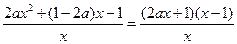 ……….….….10f
……….….….10f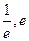 )内有且只有两个不相等的零点, 只须
)内有且只有两个不相等的零点, 只须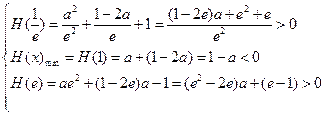 ……………..…13f
……………..…13f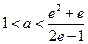 , 所以a的取值范围是(1,
, 所以a的取值范围是(1, 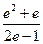 ) …………………… …..14f
) …………………… …..14f

科目:高中数学 来源:不详 题型:解答题
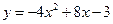 。
。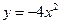 的图像经过怎样平移得来;
的图像经过怎样平移得来; )求函数的最大值或最小值;
)求函数的最大值或最小值;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
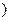 上是增函数.
上是增函数.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 设函数
设函数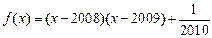 ,有 ( )
,有 ( )| A.在定义域内无零点; |
B.存在两个零点,且分别在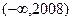 、 、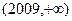 内; 内; |
C.存在两个零点,且分别在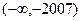 、 、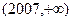 内; 高#考#资#源# 内; 高#考#资#源# |
D.存在两个零点,都在 内。 内。 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com