
分析 由题意求出AB的垂直平分线方程,和已知直线方程联立,求出圆心坐标,进一步求出半径的平方,则圆的方程可求.
解答 解:∵A(0,2)、B(-2,1),
∴AB的中点坐标为(-1,$\frac{3}{2}$),${k}_{AB}=\frac{1-2}{-2-0}=\frac{1}{2}$,
∴AB的垂直平分线方程为y-$\frac{3}{2}$=-2(x+1),
整理得:4x+2y+1=0.
联立$\left\{\begin{array}{l}{x-3y-10=0}\\{4x+2y+1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{17}{14}}\\{y=-\frac{41}{14}}\end{array}\right.$.
∴圆心坐标为($\frac{17}{14},-\frac{41}{14}$),
${r}^{2}=(\frac{17}{14}-0)^{2}+(-\frac{41}{14}-2)^{2}$=$\frac{5050}{196}$.
∴所求圆的标准方程为$(x-\frac{17}{14})^{2}+(y+\frac{41}{14})^{2}=\frac{5050}{196}$.
点评 本题考查圆的标准方程的求法,考查了数学转化思想方法,考查了计算能力,是中档题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 一定在直线y=qx-a上 | B. | 一定在直线y=ax+q上 | ||
| C. | 一定在直线y=ax-q上 | D. | 一定在直线y=qx+a上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
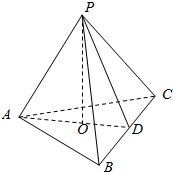 如图,在三棱锥P-ABC中,AB=AC,D是BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2.
如图,在三棱锥P-ABC中,AB=AC,D是BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com