

分析 (1)利用待定系数法,可求出种植成本与时间的函数关系式Q=g(t),和市场售价与时间的函数关系式P=f(t);
(2)由(1)知,纯收益y=P-Q,结合二次函数的图象和性质,可得答案.
解答 解:(1)由已知中函数图象的顶点坐标为(150,100)可设函数解析式为:
Q=g(t)=a(t-150)2+100,
将(100,150)代入得:a=$\frac{1}{50}$,
故Q=g(t)=$\frac{1}{50}$(t-150)2+100,(0≤t≤200),
由已知中一次函数图象交y轴于(0,300)点,
故设P=f(t)=kt+300,
将(200,100)代入得:k=-1,
故P=f(t)=-t+300,(0≤t≤200),
(2)由(1)知,纯收益y=P-Q=-t+300-[$\frac{1}{50}$(t-150)2+100]=-$\frac{1}{50}$t2+5t-250,(0≤t≤200),
故当t=125时,y取最大值62.5,
即125后上市收益最大.
点评 本题考查的知识点是函数模型的选择与应用,二次函数和一次函数的图象和性质,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{n^3}$ | B. | $\frac{4}{n^3}$ | C. | $\frac{8}{n^3}$ | D. | $\frac{1}{n^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -10 | B. | -9 | C. | 10 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
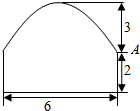 一条隧道横截面由一段抛物线及矩形的三边围成,各段长度见图中所示(单位:米),某卡车空载时可通过此隧道.
一条隧道横截面由一段抛物线及矩形的三边围成,各段长度见图中所示(单位:米),某卡车空载时可通过此隧道.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com