
| A. | (-5,5) | B. | (5,-5) | C. | (-3,3) | D. | (3,-3) |
分析 设$\overrightarrow{b}$=(x,y),由$\overrightarrow a=(2,-1),向量\overrightarrow b满足2\overrightarrow a-\overrightarrow b$=(-1,3),利用平面向量坐标运算法则能求出$\overrightarrow{b}$.
解答 解:设$\overrightarrow{b}$=(x,y),
∵$\overrightarrow a=(2,-1),向量\overrightarrow b满足2\overrightarrow a-\overrightarrow b$=(-1,3),
∴(4-x,-2-y)=(-1,3),
∴$\left\{\begin{array}{l}{4-x=-1}\\{-2-y=3}\end{array}\right.$,解得x=5,y=-5,
∴$\overrightarrow{b}$=(5,-5).
故选:B.
点评 本题考查向量的求法,是基础题,解题时要认真审题,注意平面向量坐标运算法则的合理运用.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ | B. | $\frac{x^2}{4}+{y^2}=1$ | C. | ${x^2}+\frac{y^2}{4}=1$ | D. | $\frac{{x}^{2}}{2}$+$\frac{y^2}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{2}{3}$) | B. | [0,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,+∞) | D. | (0,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{1}{32}$ | B. | x=$\frac{1}{2}$ | C. | y=2 | D. | y=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
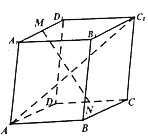 已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.
已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{4}{3}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
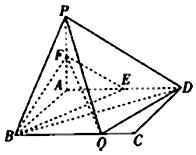 如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD.
如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com