
分析 (1)由求导公式和法则求出导数,再由题意和导数的几何意义得f(2)和f′(2),代入对应的解析式列出方程,再求解可得f(x)的解析式,求出导数,令导数大于0,可得增区间,令导数小于0,可得减区间;
(2)取曲线上任一点,求出切线的斜率和切线方程,并求与x=1和y=x的交点,再由面积公式,即可得到定值.
解答 解:(1)函数f(x)=ax+$\frac{1}{x+b}$,则f′(x)=a-$\frac{1}{(x+b)^{2}}$,
∵在点(2,f(2))处的切线方程为y=3,
∴f′(2)=a-$\frac{1}{(2+b)^{2}}$=0 ①
f(2)=2a+$\frac{1}{2+b}$=3 ②
由①②解得,a=1,b=-1,
∴f(x)=x+$\frac{1}{x-1}$,
即有f′(x)=1-$\frac{1}{(x-1)^{2}}$=$\frac{{x}^{2}-2x}{(x-1)^{2}}$,
令f′(x)>0,解得x>2或x<0,
令f′(x)<0,解得0<x<1或1<x<2,
则f(x)的增区间为(-∞,0),(2,+∞);减区间为(0,1),(1,2);
(2)∵f(x)=x+$\frac{1}{x-1}$,
∴f′(x)=1-$\frac{1}{(x-1)^{2}}$,
在曲线上任取一点(x0,x0+$\frac{1}{{x}_{0}-1}$),
由f′(x0)=1-$\frac{1}{({x}_{0}-1)^{2}}$,
知过此点的切线方程为y-x0-$\frac{1}{{x}_{0}-1}$=[1-$\frac{1}{({x}_{0}-1)^{2}}$](x-x0),
令x=1得y=$\frac{{x}_{0}+1}{{x}_{0}-1}$,即切线与直线x=1的交点为(1,$\frac{{x}_{0}+1}{{x}_{0}-1}$),
令y=x,得y=2x0-1,
即切线与直线y=x的交点为(2x0-1,2x0-1),
又直线x=1与直线y=x的交点为(1,1),
从而所围成的三角形面积为:$\frac{1}{2}$|$\frac{{x}_{0}+1}{{x}_{0}-1}$-1|•|2x0-1-1|=$\frac{1}{2}$|$\frac{2}{{x}_{0}-1}$|•|2x0-2|=2,
故所围成的三角形面积为定值2.
点评 本题考查导数知识的运用:求切线的斜率和单调区间,考查三角形面积的计算,正确求导和确定切线方程是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x)=f(x) | B. | f′(x)>f(x) | C. | f′(x)≤f(x) | D. | f′(x)≥f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f2(x)<f(x2)<f(x) | B. | f(x2)<f2(x)<f(x) | C. | f(x)<f(x2)<f2(x) | D. | f(x2)<f(x)<f2(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
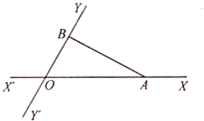 如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.
如图,有两条相交成60°角的直路XX′,YY′,交点是O,甲和乙同时从点O出发,甲沿着OX的方向,乙沿着OY的方向,经过若干小时后,甲到达点A,乙到达点B,此时甲测得他走过的路程比他到乙的距离多2km,且乙走过的路程超过4km,设甲到达点A,乙到达点B时,乙走过的路程为x km,甲走过的路程为y km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com