
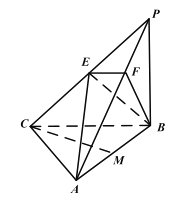
【题目】在三棱锥![]() 中,
中, ![]() 底面
底面![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)由PB⊥底面ABC,可证AC⊥PB,由∠BCA=90°,可得AC⊥CB.又PB∩CB=B,即可证明AC⊥平面PBC.
(2)取AF的中点G,连结CG,GM.可得EF∥CG.又CG平面BEF,有EF平面BEF,有CG∥平面BEF,同理证明GM∥平面BEF,有平面CMG∥平面BEF,即可证明CM∥平面BEF.
(3)取BC中点D,连结ED,可得ED∥PB,由PB⊥底面ABC,故ED⊥底面ABC,由PB=BC=CA=2,即可求得三棱锥E-ABC的体积.
试题解析:
(1)因为![]() 底面
底面![]() ,且
,且![]() 底面
底面![]() ,
,
所以![]() .
.
由![]() ,可得
,可得![]() .
.
又![]() ,
,
所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 中点.
中点.
在![]() 中,
中, ![]() 分别为
分别为![]() 中点.
中点.
所以![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
同理可证![]() 平面
平面![]() .
.
又![]() ,
,
所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(3)取![]() 中点
中点![]() ,连接
,连接![]() .
.
在![]() 中,
中, ![]() 分别为中点,所以
分别为中点,所以![]() ,
,
因为![]() 底面
底面![]() ,所以
,所以![]() 底面
底面![]() .
.
由![]() ,可得
,可得![]() .
.



科目:高中数学 来源: 题型:
【题目】商家生产一种产品,需要先进行市场调研,计划对天津、成都、深圳三地进行市场调研,待调研结束后决定生产的产品数量,下列四种方案中最可取的是( )
A.![]()
B.![]()
C.![]()
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知:f(x)=(2-x)![]() +a(x-1)2 (a∈R)
+a(x-1)2 (a∈R)
(1)讨论函数f(x)的单调区间:
(2)若对任意的x∈R,都有f(x)≤2![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 分别是定义在R上的奇函数和偶函数,当 x<0 时, f'(x)g(x)<f(x)g'(x),且 f(-3)=0 则不等式
分别是定义在R上的奇函数和偶函数,当 x<0 时, f'(x)g(x)<f(x)g'(x),且 f(-3)=0 则不等式![]() 的解集为( )
的解集为( )
A.(-∞,-3)∪(3,+∞)
B.(-3,0)∪(0,3)
C.(-3,0)∪(3,+∞)
D.(-∞,-3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班20名同学某次数学测试的成绩可绘制成如图茎叶图.由于其中部分数据缺失,故打算根据茎叶图中的数据估计全班同学的平均成绩.


(1)完成频率分布直方图;
(2)根据(1)中的频率分布直方图估计全班同学的平均成绩![]() (同一组中的数据用改组区间的中点值作代表);
(同一组中的数据用改组区间的中点值作代表);
(3)根据茎叶图计算出的全班的平均成绩为![]() ,并假设
,并假设![]() ,且
,且![]() 取得每一个可能值的机会相等,在(2)的条件下,求概率
取得每一个可能值的机会相等,在(2)的条件下,求概率![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com