
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求圆![]() 的直角坐标方程;
的直角坐标方程;
(II)若![]() 是直线
是直线![]() 与圆面
与圆面![]() 的公共点,求
的公共点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)利用极坐标与直角坐标的互化公式,即可求解圆![]() 的普通方程;
的普通方程;
(Ⅱ)解法一:设![]() ,将直线
,将直线![]() 的参数方程代入
的参数方程代入![]() ,得
,得![]() ,又由直线
,又由直线![]() 过
过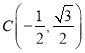 ,圆
,圆![]() 的半径是
的半径是![]() ,即求解
,即求解![]() 的范围,进而得到
的范围,进而得到![]() 的取值范围;
的取值范围;
解法二:求得直线![]() 与圆
与圆![]() 的交点为
的交点为![]() 的坐标,由点
的坐标,由点![]() 在线段
在线段![]() 上,得
上,得![]() 的最大值和最小值,即可得到
的最大值和最小值,即可得到![]() 的取值范围.
的取值范围.
试题解析:
(Ⅰ)∵圆![]() 的极坐标方程为
的极坐标方程为
![]()
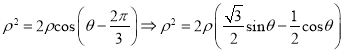
又![]() ,
,
![]() ∴圆
∴圆![]() 的普通方程为
的普通方程为![]()
(Ⅱ)解法一:设![]() ,圆
,圆![]() 的方程
的方程![]() 即
即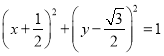 ,
,
∴圆![]() 的圆心是
的圆心是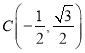 ,半径
,半径![]()
将直线![]() 的参数方程
的参数方程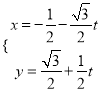 (
(![]() 为参数)代入
为参数)代入![]() ,得
,得![]()
又∵直线![]() 过
过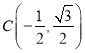 ,圆
,圆![]() 的半径是1,
的半径是1,
![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
解法二:圆![]() 的方程
的方程![]() 即
即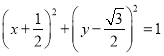 ,
,
将直线![]() 的参数方程
的参数方程 (
(![]() 为参数)化为普通方程:
为参数)化为普通方程: ![]()
∴直线![]() 与圆
与圆![]() 的交点为
的交点为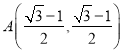 和
和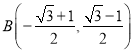 ,故点
,故点![]() 在线段
在线段![]() 上
上
从而当![]() 与点
与点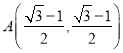 重合时,
重合时, ![]() ;
;
当![]() 与点
与点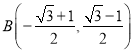 重合时,
重合时, ![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 都是定义域为
都是定义域为![]() 的连续函数.已知:
的连续函数.已知:![]() 满足:①当
满足:①当![]() 时,
时,![]() 恒成立;②
恒成立;②![]() 都有
都有![]() .
.![]() 满足:①
满足:①![]() 都有
都有![]() ;②当
;②当![]() 时,
时,![]() .若关于
.若关于![]() 的不等式
的不等式![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
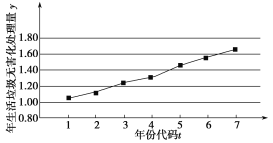
【题目】如图是我国2012年至2018年生活垃圾无害化处理量(单位:亿吨)的折线图.注:年份代码1~7分别对应年份2012~2018.
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数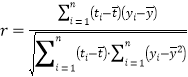 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为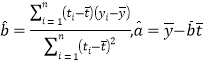 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程![]() 关于时间
关于时间![]() 的函数关系式分别为
的函数关系式分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,有以下结论:
,有以下结论:
①当![]() 时,甲走在最前面;
时,甲走在最前面;
②当![]() 时,乙走在最前面;
时,乙走在最前面;
③当![]() 时,丁走在最前面,当
时,丁走在最前面,当![]() 时,丁走在最后面;
时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点,![]() ,PA=AC=1.
,PA=AC=1.
(1)求证:AE⊥PB;
(2)求三棱锥C-ABE的体积.
(3)求二面角A-PB-C的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校研究性学习小组从汽车市场上随机抽取![]() 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于![]() 公里和
公里和![]() 公里之间,将统计结果分成
公里之间,将统计结果分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)求续驶里程在![]() 的车辆数;
的车辆数;
(3)若从续驶里程在![]() 的车辆中随机抽取
的车辆中随机抽取![]() 辆车,求其中恰有一辆车的续驶里程在
辆车,求其中恰有一辆车的续驶里程在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com