
【题目】某小区楼顶成一种“楔体”形状,该“楔体”两端成对称结构,其内部为钢架结构(未画出全部钢架,如图1所示,俯视图如图2所示),底面![]() 是矩形,
是矩形,![]() 米,
米,![]() 米,屋脊
米,屋脊![]() 到底面
到底面![]() 的距离即楔体的高为1.5米,钢架所在的平面
的距离即楔体的高为1.5米,钢架所在的平面![]() 与
与![]() 垂直且与底面的交线为
垂直且与底面的交线为![]() ,
,![]() 米,
米,![]() 为立柱且O是
为立柱且O是![]() 的中点.
的中点.
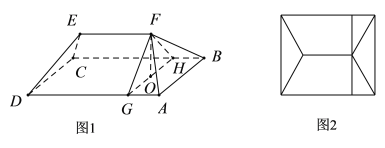
(1)求斜梁![]() 与底面
与底面![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求此模体![]() 的体积.
的体积.
【答案】(1)![]() ;(2)350(立方米).
;(2)350(立方米).
【解析】
(1)连接![]() ,由题可知
,由题可知![]() 平面
平面![]() ,
, ![]() 是直线
是直线![]() 与底面
与底面![]() 所成角,由俯视图可知,
所成角,由俯视图可知,![]() ,在
,在![]() 中进行计算即可得解;
中进行计算即可得解;
(2)由题可知,该“楔体”两端成对称结构,钢架所在的平面![]() 与
与![]() 垂直,结合俯视图可知,可将该“楔体”分割成一个直三棱柱和两个相同的四棱锥,然后由题中条件结合椎体和柱体体积公式计算即可.
垂直,结合俯视图可知,可将该“楔体”分割成一个直三棱柱和两个相同的四棱锥,然后由题中条件结合椎体和柱体体积公式计算即可.
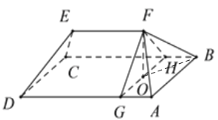
(1)如下图,连接![]() ,依题意
,依题意![]() 为立柱,即
为立柱,即![]() 平面
平面![]() ,
,
则![]() 是直线
是直线![]() 与底面
与底面![]() 所成角,
所成角,
由俯视图可知,![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
则斜梁![]() 与底面
与底面![]() 所成角的大小为
所成角的大小为![]() ;
;
(2)依题意,该“楔体”两端成对称结构,钢架所在的平面![]() 与
与![]() 垂直,结合俯视图可知,可将该“楔体”分割成一个直三棱柱和两个相同的四棱锥,
垂直,结合俯视图可知,可将该“楔体”分割成一个直三棱柱和两个相同的四棱锥,
则直三棱柱的体积
![]()
![]() (立方米),
(立方米),
两个四棱锥的体积
![]()
![]() (立方米),
(立方米),
则所求的楔体![]() 的体积
的体积![]() (立方米).
(立方米).


科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.
(1)一研究团队统计了某地区1000名患者的相关信息,得到如下表格,

该传染病的潜伏期受诸多因素影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关
潜伏期≤6天 | 潜伏期>6天 | 总计 | |
50岁以上(含50岁) | 100 | ||
50岁以下 | 55 | ||
总计 | 200 |
(2)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立.为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:下面的临界值表仅供参考.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
(参考公式: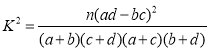 ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车进驻城市,绿色出行引领时尚.某市有统计数据显示,2020年该市共享单车用户年龄等级分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示.若将共享单车用户按照年龄分为“年轻人”(20岁-39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”,使用次数为5次或不足5次的称为“不常使用单车用户”.已知在“经常使用单车用户”中有![]() 是“年轻人”.
是“年轻人”.
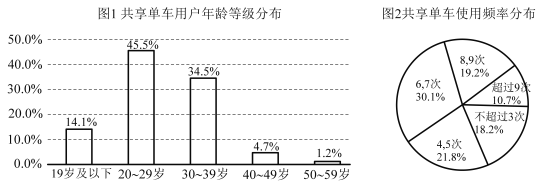
(1)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列![]() 列联表,并根据列联表的独立性检验,判断是否有85%的把握认为经常使用共享单车与年龄有关?
列联表,并根据列联表的独立性检验,判断是否有85%的把握认为经常使用共享单车与年龄有关?
年轻人 | 非年轻人 | 合计 | |
经常使用单车用户 | 120 | ||
不常使用单车用户 | 80 | ||
合计 | 160 | 40 | 200 |
使用共享单车情况与年龄列联表
(2)将(1)中频率视为概率,若从该市市民中随机任取3人,设其中经常使用共享单车的“非年轻人”人数为随机变量![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
参考数据:独立性检验界值表
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
其中,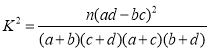 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的右焦点为
的右焦点为![]() ,过焦点
,过焦点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点(异于长轴端点),
两点(异于长轴端点),![]() 是直线
是直线![]() 上的动点.
上的动点.

(1)若直线![]() 平分线段
平分线段![]() ,求证:
,求证:![]() .
.
(2)若直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 、
、![]() 、
、![]() 的斜率成等差数列,求实数
的斜率成等差数列,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
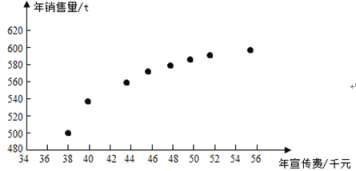
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费
(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )数据作了初步处理,得到下面的散点图及一些统计量的值.
)数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1.469 | 108.8 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?给出判断即可,不必说明理由
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?给出判断即可,不必说明理由
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x、y的关系为![]() 根据(2)的结果回答下列问题:
根据(2)的结果回答下列问题:
①年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
②年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: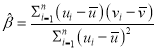 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,与坐标轴分别交于A,B两点,且经过点Q(
,与坐标轴分别交于A,B两点,且经过点Q(![]() ,1).
,1).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若P(m,n)为椭圆C外一动点,过点P作椭圆C的两条互相垂直的切线l1、l2,求动点P的轨迹方程,并求△ABP面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com