
【题目】经研究,城市公交车的数量太多容易造成资源浪费,太少又难以满足乘客需求.为此,某市公交公司从某站占的40名候车乘客中随机抽取15人,将他们的候车时间(单位: ![]() )作为样本分成5组如下表:
)作为样本分成5组如下表:
组别 | 侯车时间 | 人数 |
一 |
| 2 |
二 |
| 6 |
三 |
| 2 |
四 |
| 2 |
五 |
| 3 |
(1)估计这40名乘客中侯车时间不少于20分钟的人数;
(2)若从上表侯车时间不少于10分钟的7人中选2人作进一步的问卷调查,求抽到的两人侯车时间都不少于20分钟的概率.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x.
(1)求曲线y=f(x)在点x=2处的切线方程;
(2)若过点A(1,m)(m≠﹣2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx的导函数图象关于直线x=2对称
(1)求b值;
(2)若f(x)在x=t处取得极小值,记此极小值为g(t),求g(t)的定义域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(ax2+4x+5).
(1)若f(1)<3,求a的取值范围;
(2)若a=1,求函数f(x)的值域.
(3)若f(x)的值域为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某城市有一块半径为40m的半圆形(以O为圆心,AB为直径)绿化区域,现计划对其进行改建.在AB的延长线上取点D,使OD=80m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2. 设∠AOC=x rad.
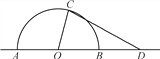
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)张强同学说:当∠AOC=![]() 时,改建后的绿化区域面积S最大.张强同学的说法正确吗?若不正确,请求出改建后的绿化区域面积S最大值.
时,改建后的绿化区域面积S最大.张强同学的说法正确吗?若不正确,请求出改建后的绿化区域面积S最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com