
【题目】已知函数f(x)=log2(x+1).
(1)将函数f(x)的图象上的所有点向右平行移动1个单位得到函数g(x)的图象,写出函数g(x)的表达式;
(2)若关于x的函数y=g2(x)﹣mg(x2)+3在[1,4]上的最小值为2,求m的值.
【答案】
(1)解:将函数f(x)的图象上的所有点向右平行移动1个单位,
得到y=log2(x﹣1+1)=log2x.
即g(x)=log2x(x>0)
(2)解: ![]() ,
,
令t=log2x(t∈[0,2])得y=t2﹣2mt+3=(t﹣m)2+3﹣m2
①若m<0,则y=t2﹣2mt+3在t∈[0,2]上递增,
∴当t=0时,ymin=3≠2,无解;
②若0≤m≤2,则当t=m时, ![]() ,解得m=1,﹣1(舍去),
,解得m=1,﹣1(舍去),
∴m=1
③若m>2,则y=t2﹣2mt+3在t∈[0,2]上递减,
∴当t=2时,ymin=7﹣4m=2,解得 ![]() ,不符合条件,舍去;
,不符合条件,舍去;
综上可得m=1
【解析】(1)根据函数图象平移关系进行求解即可.(2)利用换元法,转化为一元二次函数,利用一元二次函数单调性和最值之间的关系进行求解即可.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 ![]() .类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
.类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 . 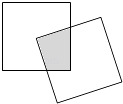
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() .
.
⑴ 求证:数列![]() 为等差数列;
为等差数列;
⑵ 设![]() ,
, ![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若当
,若当![]() 且
且![]() 为偶数时,
为偶数时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶ 设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,试求数列
,试求数列![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,函数
,函数 ![]() x.
x.
(1)若g(mx2+2x+m)的定义域为R,求实数m的取值范围;
(2)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值h(a);
(3)是否存在非负实数m、n,使得函数 ![]() 的定义域为[m,n],值域为[2m,2n],若存在,求出m、n的值;若不存在,则说明理由.
的定义域为[m,n],值域为[2m,2n],若存在,求出m、n的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)已知集合A={(x,y)|y=x2+2},B={(x,y)|y=6﹣x2},求A∩B; (Ⅱ)已知集合A={y|y=x2+2},B={y|y=6﹣x2},求A∩B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE. 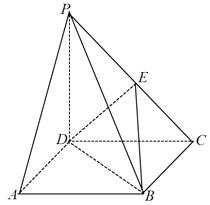
(1)证明:DE⊥平面PBC.
(2)试判断四面体EBCD是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(3)记阳马P﹣ABCD的体积为V1 , 四面体EBCD的体积为V2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. 将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后得到函数
个单位后得到函数![]() 的图象
的图象
B. 函数![]() 图象关于点
图象关于点![]() 中心对称
中心对称
C. 函数![]() 的图象关于
的图象关于![]() 对称
对称
D. 函数![]() 在区间
在区间![]() 内单调递增
内单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 由上半椭圆
由上半椭圆![]() :
: ![]() (
(![]() ,
, ![]() )和部分抛物线
)和部分抛物线![]() :
: ![]() (
(![]() )连接而成,
)连接而成, ![]() 与
与![]() 的公共点为
的公共点为![]() ,
, ![]() ,其中
,其中![]() 的离心率为
的离心率为![]() .
.

(1)求![]() ,
, ![]() 的值;
的值;
(2)过点![]() 的直线
的直线![]() 与
与![]() ,
, ![]() 分别交于点
分别交于点![]() ,
, ![]() (均异于点
(均异于点![]() ,
, ![]() ),是否存在直线
),是否存在直线![]() ,使得以
,使得以![]() 为直径的圆恰好过
为直径的圆恰好过![]() 点,若存在,求出直线
点,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com