
【题目】已知函数![]() .
.
(1)设![]() ,
,
①当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
②当![]() 时,求证:
时,求证:![]() 对任意
对任意![]() 恒成立.
恒成立.
(2)讨论![]() 的极值点个数.
的极值点个数.
【答案】(1)①![]() ;②证明见解析;(2)当
;②证明见解析;(2)当![]() 时,
时,![]() 有且仅有一个极值点;当
有且仅有一个极值点;当![]() 时,
时,![]() 有三个极值点
有三个极值点
【解析】
(1)①将![]() 代入,求出切点及斜率,利用点斜式即可得切线方程;
代入,求出切点及斜率,利用点斜式即可得切线方程;
②只需证![]() 时,
时,![]() 对任意
对任意![]() 都成立,利用导数求其最值即可得证;
都成立,利用导数求其最值即可得证;
(2)![]() 只有一个极值点或三个极值点,令
只有一个极值点或三个极值点,令![]() ,当
,当![]() 只有一个极值点时,
只有一个极值点时,![]() 的图象必穿过
的图象必穿过![]() 轴且只穿过一次,即
轴且只穿过一次,即![]() 为单调减函数或者
为单调减函数或者![]() 极值同号,分类讨论即可得解,同理可求当
极值同号,分类讨论即可得解,同理可求当![]() 有三个极值点时的情况.
有三个极值点时的情况.
解:(1)![]() ,
,
①当![]() 时,
时,![]() ,
,
∴切线方程为![]() ;
;
②证明:要证对任意![]() ,
,![]() ,
,
只需证![]() 时,
时,![]() 对任意
对任意![]() 都成立,
都成立,![]() ,
,
令![]() 得
得![]() ,
,
且![]() 时,
时,![]() 单减,
单减,![]() 时,
时,![]() 单增,
单增,![]() ,
,![]() 在
在![]() 上单增,
上单增,![]() ,
,
∴当![]() 时,
时,![]() 对任意
对任意![]() 恒成立.
恒成立.
(2)![]() ,,则
,,则![]()
![]() 只有一个极值点或三个极值点,
只有一个极值点或三个极值点,
令![]() ,当
,当![]() 只有一个极值点时,
只有一个极值点时,![]() 的图象必穿过
的图象必穿过![]() 轴且只穿过一次,即
轴且只穿过一次,即![]() 为单调减函数或者
为单调减函数或者![]() 极值同号,
极值同号,
(i)![]() 为单调减函数时,
为单调减函数时,![]() 在
在![]() 上恒成立,则
上恒成立,则![]() ,解得
,解得![]() ;
;
(ii)![]() 极值同号时,设
极值同号时,设![]() 为极值点,
为极值点,
则![]() 有解,则
有解,则![]() ,
,
且![]() ,
,![]() ,
,![]() ,
,
同理![]() ,
,![]() ,
,
化简得![]() ,
,![]() ,解得
,解得![]() ,
,
∴当![]() 时,
时,![]() 只有一个极值点;
只有一个极值点;
当![]() 有三个极值点时,
有三个极值点时,![]() ,同理可得
,同理可得![]() ,
,
综上,当![]() 时,
时,![]() 有且仅有一个极值点;当
有且仅有一个极值点;当![]() 时,
时,![]() 有三个极值点.
有三个极值点.


科目:高中数学 来源: 题型:
【题目】某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300名学生每周平均体育运动时间的样本数据(单位:小时).
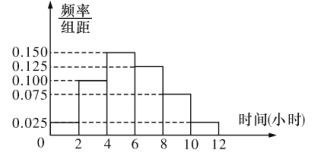
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,估计该校学生每周平均体育运动时间超过4小时的概率;
,估计该校学生每周平均体育运动时间超过4小时的概率;
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有![]() 的把握认为“该校学生的毎周平均体育运动时间与性别有关”.
的把握认为“该校学生的毎周平均体育运动时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附: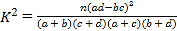 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元).这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据y(单位:十亿元),绘制如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额y | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图,如图所示
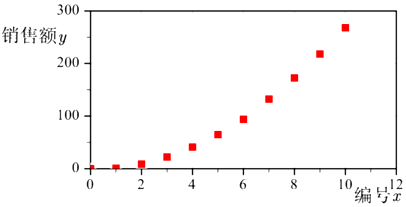
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为销售额
哪一个适宜作为销售额![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及如表中的数据,建立![]() 关于
关于![]() 的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
(3)把销售超过100(十亿元)的年份叫“畅销年”,把销售额超过200(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取2个,求至少取到一个“狂欢年”的概率.
参考数据:![]()
|
|
|
|
|
|
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别
的斜率和截距的最小二乘估计公式分别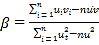 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线![]() 上任意一点,过F作TF的垂线交椭圆C于点P,Q.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当![]() 最小时,求点T的坐标.
最小时,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校![]() 名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)

将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面![]() 列联表:
列联表:
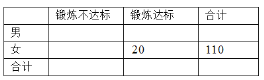
并通过计算判断,是否能在犯错误的概率不超过![]() 的前提下认为“锻炼达标”与性别有关?
的前提下认为“锻炼达标”与性别有关?
(2)在“锻炼达标”的学生中,按男女用分层抽样方法抽出![]() 人,进行体育锻炼体会交流.
人,进行体育锻炼体会交流.
(i)求这![]() 人中,男生、女生各有多少人?
人中,男生、女生各有多少人?
(ii)从参加体会交流的![]() 人中,随机选出
人中,随机选出![]() 人发言,记这
人发言,记这![]() 人中女生的人数为
人中女生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: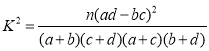 ,其中
,其中![]() .
.
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 |
0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了预测下月产品销售情况,找出了近7个月的产品销售量![]() (单位:万件)的统计表:
(单位:万件)的统计表:
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售量 |
|
|
|
|
|
|
|
但其中数据污损不清,经查证![]() ,
,![]() ,
,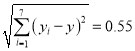 .
.
(1)请用相关系数说明销售量![]() 与月份代码
与月份代码![]() 有很强的线性相关关系;
有很强的线性相关关系;
(2)求![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)公司经营期间的广告宣传费![]() (单位:万元)(
(单位:万元)(![]() ),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
参考公式及数据:![]() ,相关系数
,相关系数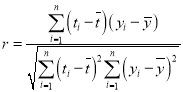 ,当
,当![]() 时认为两个变量有很强的线性相关关系,回归方程
时认为两个变量有很强的线性相关关系,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为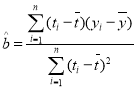 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
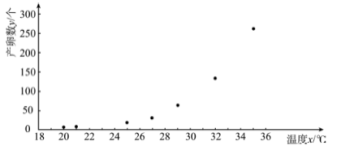
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在P地正西方向8km的A处和正东方向1km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]()
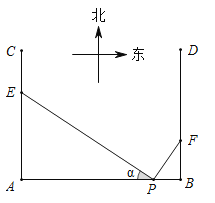
![]() Ⅰ
Ⅰ![]() 为减少对周边区域的影响,试确定E,F的位置,使
为减少对周边区域的影响,试确定E,F的位置,使![]() 与
与![]() 的面积之和最小;
的面积之和最小;
![]() Ⅱ
Ⅱ![]() 为节省建设成本,求使
为节省建设成本,求使![]() 的值最小时AE和BF的值.
的值最小时AE和BF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com