
【题目】设函数 ![]() 的定义域为
的定义域为 ![]() ,若函数
,若函数 ![]() 满足下列两个条件,则称
满足下列两个条件,则称 ![]() 在定义域
在定义域 ![]() 上是闭函数.①
上是闭函数.① ![]() 在
在 ![]() 上是单调函数;②存在区间
上是单调函数;②存在区间 ![]() ,使
,使 ![]() 在
在 ![]() 上值域为
上值域为 ![]() .如果函数
.如果函数 ![]() 为闭函数,则
为闭函数,则 ![]() 的取值范围是.
的取值范围是.
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( ) 
A.4
B.5
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,圆
中,圆 ![]() ,圆
,圆 ![]() .
.
(Ⅰ)在以 ![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,分别写出圆
轴正半轴为极轴的极坐标系中,分别写出圆 ![]() 的极坐标方程,并求出圆
的极坐标方程,并求出圆 ![]() 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求出 ![]() 与
与 ![]() 的公共弦的参数方程.
的公共弦的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥 ![]() 的底面积
的底面积 ![]() 是边长为
是边长为 ![]() 的正三角形,
的正三角形, ![]() 点在侧面
点在侧面 ![]() 内的射影
内的射影 ![]() 为
为 ![]() 的垂心,二面角
的垂心,二面角 ![]() 的平面角的大小为
的平面角的大小为 ![]() ,则
,则 ![]() 的长为( )
的长为( )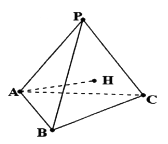
A.3
B.![]()
C.![]()
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强高考与高中学习的关联度,考生总成绩由统一高考的语文、数学、外语3个科目成绩和高中学业水平考试3个科目成绩组成.保持统一高考的语文、数学、外语科目不变,分值不变,不分文理科,外语科目提供两次考试机会.计入总成绩的高中学业水平考试科目,由考生根据报考高校要求和自身特长,在思想政治、历史、地理、物理、化学、生物、信息技术七科目中自主选择三科.
(1)某高校某专业要求选考科目物理,考生若要报考该校该专业,则有多少种选考科目的选择;
(2)甲、乙、丙三名同学都选择了物理、化学、历史组合,各学科成绩达到二级的概率都是0.8,且三人约定如果达到二级不参加第二次考试,达不到二级参加第二次考试,如果设甲、乙、丙参加第二次考试的总次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线
轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为
![]() (
(![]() 为参数,
为参数, ![]() 为直线的倾斜角).
为直线的倾斜角).
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 有唯一的公共点,求角
有唯一的公共点,求角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com