
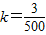 ,∴
,∴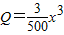 ,
,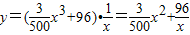 ,
,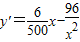 ,令y′=0得x=20,
,令y′=0得x=20,

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年高三一轮精品复习单元测试(12)数学试卷解析版 题型:解答题
(本小题满分10分)一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com