练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知关于x的一元二次方程x2﹣2ax+a+2=0，当a为何值时，该方程：
    （1）有两个不同的正根；
    （2）有不同的两根且两根在（1，3）内．

    【答案】
    （1）解：关于x的一元二次方程x2﹣2ax+a+2=0，

    当△=4a2﹣4（a+2）＞0，且x1+x2=2a＞0、x1x2=a+2＞0时，

    即当a＞2时，该方程有两个不同的正根


    （2）解：令f（x）=x2﹣2ax+a+2，则当 时，即2＜a＜ 时，

    方程x2﹣2ax+a+2=0有不同的两根且两根在（1，3）内


    【解析】（1）方程有两个不同的正根，等价于△=4a2﹣4（a+2）＞0，且x1+x2=2a＞0、x1x2=a+2＞0．由此求得a的范围．（2）令f（x）=x2﹣2ax+a+2，则当 时，满足条件，由此求得a的范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列各组函数中，f（x）与g（x）表示同一个函数的是（ ）
    A.
    B.
    C.f（x）=x，g（x）=（x﹣1）0
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图： 是平行四边行， 平面, // , ， ， 。

    （1）求证： //平面；

    （2）求证：平面平面；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC﹣A1B1C1中，AA1⊥平面ABC，AB=AA1=2，AC= ，BC=3，M，N分别为B1C1、AA1的中点．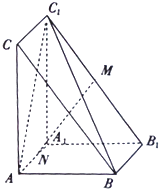

    （1）求证：平面ABC1⊥平面AA1C1C；
    （2）求证：MN∥平面ABC1 ， 并求M到平面ABC1的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】经过原点的直线与椭圆交于两点，点为椭圆上不同于的一点，直线的斜率均存在，且直线的斜率之积为.

    （1）求椭圆的离心率；

    （2）设分别为椭圆的左、右焦点，斜率为的直线经过椭圆的右焦点，且与椭圆交于两点.若点在以为直径的圆内部，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，焦点在x轴上的椭圆 =1（a＞0）的左、右焦点分别为F1、F2 ， P是椭圆上位于第一象限内的一点，且直线F2P与y轴的正半轴交于A点，△APF1的内切圆在边PF1上的切点为Q，若|F1Q|=4，则该椭圆的离心率为（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】盒内有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球.规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得分，现从盒内任取3个球.

    (Ⅰ)求取出的3个球中至少有一个红球的概率；

    (Ⅱ)求取出的3个球得分之和恰为1分的概率；

    (Ⅲ)设为取出的3个球中白色球的个数，求的分布列及期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的方程为 =1，其左右焦点分别为F1 ， F2 ， 过其左焦点且斜率为1的直线与该椭圆相交与A，B两点，则 = ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

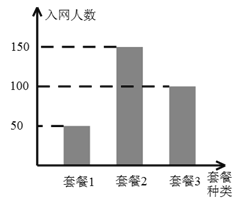
    【题目】移动公司在春节正月初八这天推出4G套餐，对这天办理套餐的客户进行优惠，优惠方案如下：选择套餐一的客户可获得优惠200元，选择套餐二的客户可获得优惠500元，选择套餐三的客户可获得优惠300元. 初八当天参与活动的人数统计结果如图所示，

    （Ⅰ）从参加当天活动的人中任选一人，求此人获得优惠金额不低于300元的概率（将频率视为概率）；

    （Ⅱ）若采用分层抽样的方式从参加活动的客户中选出6人，再从该6人中随机选两人，求这两人获得相等优惠金额的概率.

    查看答案和解析>>

    同步练习册答案