【题目】已知直线l：mx﹣y=1，若直线l与直线x﹣（m﹣1）y=2垂直，则m的值为 ， 动直线l：mx﹣y=1被圆C：x2﹣2x+y2﹣8=0截得的最短弦长为 ．
【答案】
；2 
【解析】解：∵直线l：mx﹣y=1，直线l与直线x﹣（m﹣1）y=2垂直，
∴m×1+（﹣1）×[﹣（m﹣1）]=0，
解得m= 
．
∵圆C：x2﹣2x+y2﹣8=0的圆心C（1，0），半径r= 
=3，
圆心C（1，0）到直线l：mx﹣y=1的距离d= 
，
∴弦长为：2 
=2 
=2 
，
∴当且仅当m=﹣1时，动直线l：mx﹣y=1被圆C：x2﹣2x+y2﹣8=0截得的最短弦长为2 
．
所以答案是： 
．
【考点精析】利用直线与圆的三种位置关系对题目进行判断即可得到答案，需要熟知直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】已知直线l的参数方程为 
（t为参数），曲线C的参数方程为 
（θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，点P的极坐标为（2 
， 
）．
（Ⅰ）求直线l以及曲线C的极坐标方程；
（Ⅱ）设直线l与曲线C交于A，B两点，求△PAB的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=sinx，x∈（0，2π），点P（x，y）是函数f（x）图象上任一点，其中0（0，0），A（2π，0），记△OAP的面积为g（x），则g′（x）的图象可能是（ ）
A.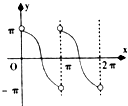
B.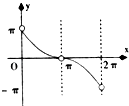
C.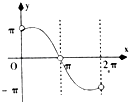
D.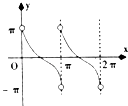
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=m﹣|x﹣2|，m∈R，且f（x+2）≥0的解集为[﹣1，﹣1]．
（1）求m的值；
（2）若a，b，c∈R，且 
+ 
+ 
=m，求证：a2+b2+c2≥36．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线l：x＋2y－2＝0，试求：
（1）点P(－2，－1)关于直线l的对称点坐标；
（2）直线 
关于直线l对称的直线l2的方程；
（3）直线l关于点(1，1)对称的直线方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】直线l1 ， l2分别是函数f（x）=sinx，x∈[0，π]图象上点P1 ， P2处的切线，l1 ， l2垂直相交于点P，且l1 ， l2分别与y轴相交于点A，B，则△PAB的面积为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
