
【题目】某企业质量检验员为了检测生产线上零件的质量情况,从生产线上随机抽取了![]() 个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
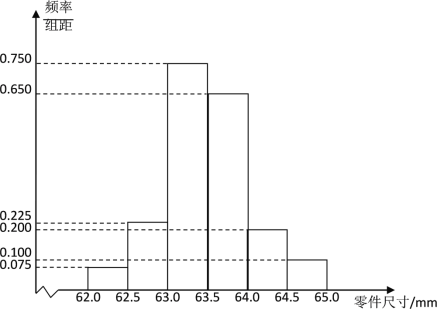
(1)根据频率分布直方图,求这![]() 个零件尺寸的中位数(结果精确到
个零件尺寸的中位数(结果精确到![]() );
);
(2)若从这![]() 个零件中尺寸位于
个零件中尺寸位于![]() 之外的零件中随机抽取
之外的零件中随机抽取![]() 个,设
个,设![]() 表示尺寸在
表示尺寸在![]() 上的零件个数,求
上的零件个数,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)已知尺寸在![]() 上的零件为一等品,否则为二等品,将这
上的零件为一等品,否则为二等品,将这![]() 个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱
个零件尺寸的样本频率视为概率. 现对生产线上生产的零件进行成箱包装出售,每箱![]() 个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为
个. 企业在交付买家之前需要决策是否对每箱的所有零件进行检验,已知每个零件的检验费用为![]() 元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付
元. 若检验,则将检验出的二等品更换为一等品;若不检验,如果有二等品进入买家手中,企业要向买家对每个二等品支付![]() 元的赔偿费用. 现对一箱零件随机抽检了
元的赔偿费用. 现对一箱零件随机抽检了![]() 个,结果有
个,结果有![]() 个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
个二等品,以整箱检验费用与赔偿费用之和的期望值作为决策依据,该企业是否对该箱余下的所有零件进行检验?请说明理由.
【答案】(1)![]() ;(2)分布列见详解,期望为
;(2)分布列见详解,期望为![]() ;(3)余下所有零件不用检验,理由见详解.
;(3)余下所有零件不用检验,理由见详解.
【解析】
(1)计算![]() 的频率,并且与
的频率,并且与![]() 进行比较,判断中位数落在的区间,然后根据频率的计算方法,可得结果.
进行比较,判断中位数落在的区间,然后根据频率的计算方法,可得结果.
(2)计算位于![]() 之外的零件中随机抽取
之外的零件中随机抽取![]() 个的总数,写出
个的总数,写出![]() 所有可能取值,并计算相对应的概率,列出分布列,计算期望,可得结果.
所有可能取值,并计算相对应的概率,列出分布列,计算期望,可得结果.
(3)计算整箱的费用,根据余下零件个数服从二项分布,可得余下零件个数的期望值,然后计算整箱检验费用与赔偿费用之和的期望值,进行比较,可得结果.
(1)尺寸在![]() 的频率:
的频率:
![]()
尺寸在![]() 的频率:
的频率:![]()
且![]()
所以可知尺寸的中位数落在![]()
假设尺寸中位数为![]()
所以![]()
所以这![]() 个零件尺寸的中位数
个零件尺寸的中位数![]()
(2)尺寸在![]() 的个数为
的个数为![]()
尺寸在![]() 的个数为
的个数为![]()
![]() 的所有可能取值为1,2,3,4
的所有可能取值为1,2,3,4
则![]() ,
,![]()
![]() ,
,![]()
所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]()
(3)二等品的概率为![]()
如果对余下的零件进行检验则整箱的检验费用为
![]() (元)
(元)
余下二等品的个数期望值为![]()
如果不对余下的零件进行检验,
整箱检验费用与赔偿费用之和的期望值为
![]() (元)
(元)
所以![]() ,所以可以不对余下的零件进行检验.
,所以可以不对余下的零件进行检验.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
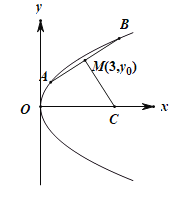
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有下列四个结论:
,有下列四个结论:
①![]() 为偶函数;②
为偶函数;②![]() 的值域为
的值域为![]() ;
;
③![]() 在
在![]() 上单调递减;④
上单调递减;④![]() 在
在![]() 上恰有8个零点,
上恰有8个零点,
其中所有正确结论的序号为( )
A.①③B.②④C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是偶函数,且在R上有导函数
是偶函数,且在R上有导函数![]() ,若对
,若对![]() 都有
都有![]() ,则关于函数
,则关于函数![]() 的四个判断:①若函数在
的四个判断:①若函数在![]() 处有定义,则
处有定义,则![]() ;②
;②![]() ;③
;③![]() 是周期函数;④若函数在
是周期函数;④若函数在![]() 处有定义,则
处有定义,则![]() .其中正确的判断有( )
.其中正确的判断有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 的图象把圆
的图象把圆![]() 的面积两等分;
的面积两等分;
②![]() 是周期为
是周期为![]() 的函数;
的函数;
③函数![]() 在区间
在区间![]() 上有
上有![]() 个零点;
个零点;
④函数![]() 在区间
在区间![]() 上单调递减.
上单调递减.
则正确结论的序号为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com