
【题目】已知cosα= ![]() ,cos(α+β)=﹣
,cos(α+β)=﹣ ![]() ,且α,β∈(0,
,且α,β∈(0, ![]() ),则cos(α﹣β)的值等于( )
),则cos(α﹣β)的值等于( )
A.﹣ ![]()
B.![]()
C.﹣ ![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosx(sinx﹣cosx)+1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间 ![]() 上的最小值和最大值.
上的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年6月22 日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在15-75岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() .把年龄落在区间
.把年龄落在区间![]() 和
和![]() 内的人分别称为 “青少年”和“中老年”.
内的人分别称为 “青少年”和“中老年”.
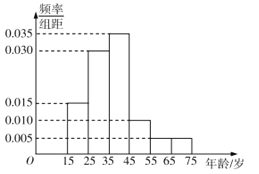
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数;
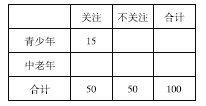
(2)根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
附:参考公式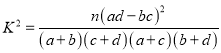 ,其中
,其中![]() .
.
临界值表:
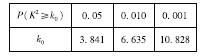
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆心坐标为( ![]() ,1)的圆M与x轴及直线y=
,1)的圆M与x轴及直线y= ![]() x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y= ![]() x分别相切于C、D两点.
x分别相切于C、D两点. 
(1)求圆M和圆N的方程;
(2)过点B作直线MN的平行线l,求直线l被圆N截得的弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC满足| ![]() |=3,|
|=3,| ![]() |=4,O是△ABC所在平面内一点,满足|
|=4,O是△ABC所在平面内一点,满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,且
|,且 ![]() =λ
=λ ![]() +
+ ![]()
![]() (λ∈R),则cos∠BAC= .
(λ∈R),则cos∠BAC= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F、G分别是棱A1B1、BB1、B1C1的中点,则下列结论中:
①FG⊥BD
②B1D⊥面EFG
③面EFG∥面ACC1A1
④EF∥面CDD1C1
正确结论的序号是( )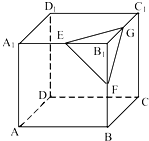
A.①和②
B.②和④
C.①和③
D.③和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的![]() 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温![]() (
(![]() )与该奶茶店的
)与该奶茶店的![]() 品牌饮料销量
品牌饮料销量![]() (杯),得到如表数据:
(杯),得到如表数据:
日期 | 1月11号 | 1月12号 | 1月13号 | 1月14号 | 1月15号 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程式
的线性回归方程式![]() ;
;
(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com