
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
分析 根据已知条件推导函数f(x)的周期,再利用函数与方程思想把问题转化,画出函数的图象,即可求解.
解答 解:∵f(x-1)=f(x+1)
∴f(x)=f(x+2),
∴原函数的周期T=2.
又∵f(x)是偶函数,
∴f(-x)=f(x).
又当x∈[-1,0]时,f(x)=-x,∴x∈[0,1]时,f(x)=x,函数的周期为2,
∴原函数的对称轴是x=1,且f(-x)=f(x+2).
设 y1=f(x),y2=lgx,x=10,y2=1
函数g(x)=f(x)-lgx在(0,10)上的零点的个数如图: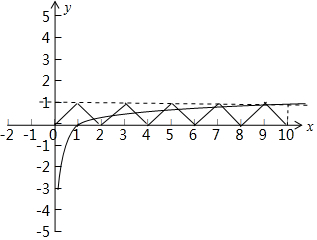
即为函数y1=f(x),y2=lgx的图象交点的个数为9个.
函数g(x)=f(x)-lgx有9个零点
故选:B.
点评 本题考查函数的性质,函数与方程思想,数形结合思想.转化思想,属中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为监测全市小学生身体形态生理机能的指标情况,体检中心从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据分成如下5个组:[100,110),[110,120),…,[140,150),并绘制成频率分布直方图(如图所示).
为监测全市小学生身体形态生理机能的指标情况,体检中心从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据分成如下5个组:[100,110),[110,120),…,[140,150),并绘制成频率分布直方图(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ③④ | C. | ②④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$或$\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$或2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com