
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
:  (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,
, ![]() ,求
,求![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知空间几何体![]() 中,
中, ![]() 与
与![]() 均为边长为
均为边长为![]() 的等边三角形,
的等边三角形, ![]() 为腰长为
为腰长为![]() 的等腰三角形,平面
的等腰三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
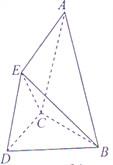
(Ⅰ)试在平面![]() 内作一条直线,使得直线上任意一点
内作一条直线,使得直线上任意一点![]() 与
与![]() 的连线
的连线![]() 均与平面
均与平面![]() 平行,并给出详细证明;
平行,并给出详细证明;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的方程是
的方程是![]() ,圆
,圆![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)分别求直线![]() 与圆
与圆![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
: ![]() (
(![]() )与圆
)与圆![]() 的交点为
的交点为![]() ,
, ![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,射线
,射线![]() :
: ![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com