
【题目】已知函数![]() (a为常数)的图象与
(a为常数)的图象与![]() 轴交于点
轴交于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]()
(1)求![]() 的值及函数
的值及函数![]() 的极值;
的极值;
(2)证明:当![]() 时,
时,![]()
【答案】(1)当x=ln2时,f(x)取得极小值,且极小值为f(ln2)=2-ln4,f(x)无极大值.(2)见解析
【解析】试题分析:(1)首先求点![]() 的坐标
的坐标![]() ,再根据
,再根据![]() ,解得
,解得![]() 的值,然后求
的值,然后求![]() 的
的![]() 值,以及两侧的单调性,根据单调性求得函数的极值;(2)设函数
值,以及两侧的单调性,根据单调性求得函数的极值;(2)设函数![]() ,根据(1)的结果可知函数单调递增,即证
,根据(1)的结果可知函数单调递增,即证![]() .
.
试题解析: (1)由f(x)=ex-ax,得f′(x)=ex-a. 又f′(0)=1-a=-1,得a=2.
所以f(x)=ex-2x,f′(x)=ex-2. 令f′(x)=0,得x=ln2.
当x<ln2时,f′(x)<0,f(x)单调递减;当x>ln2时,f′(x)>0,f(x)单调递增.
所以当x=ln2时,f(x)取得极小值,且极小值为f(ln2)=eln2-2ln2=2-ln4,f(x)无极大值.
(2)令g(x)=ex-x2,则g′(x)=ex-2x. 由(1)得g′(x)=f(x)≥f(ln2)>0,
故g(x)在R上单调递增,又g(0)=1>0,因此,当x>0时,g(x)>g(0)>0,即x2<ex.


科目:高中数学 来源: 题型:
【题目】选修4﹣1:平面几何
如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
(1)求证:∠DEA=∠DFA;
(2)若∠EBA=30°,EF= ![]() ,EA=2AC,求AF的长.
,EA=2AC,求AF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
[20,30) | 30 | 18 |
[30,40) | 36 | 24 |
[40,50) | 12 | 9 |
[50,60] | 4 | 3 |
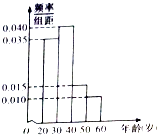
(1)若用分层抽样法从全校教师中抽取一个容量为40的样本,求从年龄段[20,30)抽取的人数;
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P(x0,y0)是函数f(x)图象上任意一点,且y02≥x02,则f(x)的解析式可以是_____.(填序号)
①f(x)=x﹣![]() ②f(x)=ex﹣1(e≈2.718,是一个重要常数)③f(x)=x+
②f(x)=ex﹣1(e≈2.718,是一个重要常数)③f(x)=x+![]() ④y=x2
④y=x2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|2x﹣a|﹣1.
①当a=0时,不等式f(x)+1>0的解集为_____;
②若函数f(x)有三个不同的零点,则实数a的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中_________为真命题.
①“A∩B=A”成立的必要条件是“A![]() B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
③“全等三角形是相似三角形”的逆命题; ④“圆内接四边形对角互补”的逆否命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com