
 ,(a,b为常数).当x>0时,F(x)=f(x),且F(x)为R上的奇函数.
,(a,b为常数).当x>0时,F(x)=f(x),且F(x)为R上的奇函数.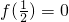 ,且f(x)的最小值为0,求F(x)的表达式;
,且f(x)的最小值为0,求F(x)的表达式; 在[2,4]上是单调函数,求k的取值范围.
在[2,4]上是单调函数,求k的取值范围.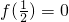 得a-b+1=0,
得a-b+1=0, ,知a=1,b=2.
,知a=1,b=2.
 =
= .x∈[2,4].
.x∈[2,4]. ,t∈[1,2].
,t∈[1,2]. 或
或 时,y为单调函数.
时,y为单调函数.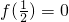 可消去b,再由f(x)的最小值为0确定f(x)的解析式,最后求出F(x)的解析式.
可消去b,再由f(x)的最小值为0确定f(x)的解析式,最后求出F(x)的解析式. ,再将t=log2x代入进行换元,可得答案.
,再将t=log2x代入进行换元,可得答案.

科目:高中数学 来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版) 题型:解答题
 (a,b为常数),且方程
(a,b为常数),且方程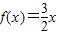 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2,查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版) 题型:解答题
 (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2,查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省郑州市新密二高高三(上)第一次月考数学试卷(解析版) 题型:解答题
 (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2,查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省株洲二中高三(下)第十次月考数学试卷(文科)(解析版) 题型:解答题
 ,(a,b为常数).当x>0时,F(x)=f(x),且F(x)为R上的奇函数.
,(a,b为常数).当x>0时,F(x)=f(x),且F(x)为R上的奇函数. ,且f(x)的最小值为0,求F(x)的表达式;
,且f(x)的最小值为0,求F(x)的表达式; 在[2,4]上是单调函数,求k的取值范围.
在[2,4]上是单调函数,求k的取值范围.查看答案和解析>>
科目:高中数学 来源:2012年云南省曲靖市宣威市高三第一次调研摸底数学试卷(理科)(解析版) 题型:解答题
 (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com