
【题目】已知直线![]() ⊥平面
⊥平面![]() 垂足为
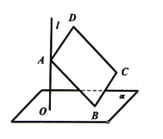
垂足为![]() 在矩形ABCD中,AD=1,AB=2,若点A在
在矩形ABCD中,AD=1,AB=2,若点A在![]() 上移动,点B在平面
上移动,点B在平面![]() 上移动,则
上移动,则![]() D两点间的最大距离为_______.
D两点间的最大距离为_______.
【答案】1![]()
【解析】
先将原问题转化为平面内的最大距离问题解决,以O为原点,OA为y轴,OB为x轴建立直角坐标系,如图.设∠ABO=θ,D(x,y),D、O两点间的最大距离表示成2![]() sin(2θ
sin(2θ![]() )+3,最后结合三角函数的性质求出其最大值即可.
)+3,最后结合三角函数的性质求出其最大值即可.
将原问题转化为平面内的最大距离问题解决,AD=1,AB=2,
以O为原点,OA为y轴,OB为x轴建立直角坐标系,如图.
设∠ABO=θ,D(x,y),则有:
x=ADsinθ=sinθ,
y=ABsinθ+ADcosθ
=cosθ+2sinθ,
∴x2+y2=sin2θ+cos2θ+4sinθcosθ+4sin2θ.
=﹣2cos2θ+2sin2θ+3
=2![]() sin(2θ
sin(2θ![]() )+3,
)+3,
当sin(2θ![]() )=1时,x2+y2最大,为2
)=1时,x2+y2最大,为2![]() 3,
3,
则D、O两点间的最大距离为1![]() .
.
故答案为1![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,∠ABC=![]() ,D是棱AC的中点,且AB=BC=BB1=2.
,D是棱AC的中点,且AB=BC=BB1=2.

(1)求证:AB1∥平面BC1D;
(2)求异面直线AB1与BC1的夹角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马.如图所示,在阳马![]() 中,
中,![]() 底面
底面![]() .
.

(1)若![]() ,斜梁
,斜梁![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求立柱
,求立柱![]() 的长(精确到
的长(精确到![]() );
);
(2)证明:四面体![]() 为鳖臑;
为鳖臑;
(3)若![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一个动点,求
上一个动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是平面内互不平行的三个向量,
是平面内互不平行的三个向量,![]() ,有下列命题:
,有下列命题:
①方程![]() 不可能有两个不同的实数解;
不可能有两个不同的实数解;
②方程![]() 有实数解的充要条件是
有实数解的充要条件是![]() ;
;
③方程![]() 有唯一的实数解
有唯一的实数解![]() ;
;
④方程![]() 没有实数解.
没有实数解.
其中真命题有 .(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥
中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥![]() 的体积为
的体积为![]()
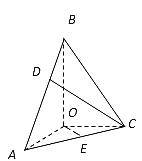
(1)求三棱锥![]() 的高;
的高;
(2)在线段AB上取一点D,当D在什么位置时,![]() 和
和![]() 的夹角大小为
的夹角大小为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax-alnx(a∈R).
(1)若函数f(x)在x=1处取得极值,求a的值;
(2)在(1)的条件下,求证:f(x)≥-![]() +
+![]() -4x+
-4x+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
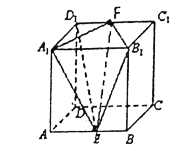
【题目】已知正方体![]() 的棱长为4,E、F分别是棱AB、
的棱长为4,E、F分别是棱AB、![]() 的中点,联结EF、
的中点,联结EF、![]() 、
、![]() 、
、![]() E、
E、![]() E、
E、![]() E.
E.
![]() 求三棱锥
求三棱锥![]() 的体积;
的体积;
![]() 求直线
求直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小![]() 结果用反三角函数值表示
结果用反三角函数值表示![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com