
【题目】已知函数![]() .
.
(1)若![]() 是
是![]() 的导函数,讨论
的导函数,讨论![]() 的单调性;
的单调性;
(2)若![]() (
(![]() 是自然对数的底数),求证:
是自然对数的底数),求证:![]() .
.
【答案】(1)①当![]() 时,
时,![]() 在
在![]() 上是增函数;②当
上是增函数;②当![]() 时,
时,![]() 在
在![]() 上是增函数;在
上是增函数;在![]() 上是减函数。(2)证明见解析。
上是减函数。(2)证明见解析。
【解析】
(1)求出![]() ,得
,得![]() ,然后求出导函数
,然后求出导函数![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数g
的范围,可得函数g![]() 增区间,g
增区间,g![]() 求得
求得![]() 的范围,可得函数g
的范围,可得函数g![]() 的减区间;(2)因为
的减区间;(2)因为![]() ,令
,令![]() ,再次求导可证明
,再次求导可证明![]() 在区间
在区间![]() 上有唯一零点
上有唯一零点![]() ,在区间
,在区间![]() 上,
上,![]() 是减函数,在区间
是减函数,在区间![]() 上,
上,![]() 是增函数,故当
是增函数,故当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,只需证明
,只需证明![]() 即可.
即可.
(1)因为![]() ,所以
,所以![]() ,
,
![]()
![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数;
上是增函数;
②当![]() 时,由
时,由![]() 得
得![]() ,
,
所以![]() 在
在![]() 上是增函数;在
上是增函数;在![]() 上是减函数;
上是减函数;
(2)因为![]() ,令
,令![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() 在
在![]() 是增函数,
是增函数,
下面证明![]() 在区间
在区间![]() 上有唯一零点
上有唯一零点![]() ,
,
因为![]() ,
,![]() ,
,
又因为![]() ,所以
,所以![]() ,
,![]() ,
,
由零点存在定理可知,![]() 在区间
在区间![]() 上有唯一零点
上有唯一零点![]() ,
,
在区间![]() 上,
上,![]() ,
,![]() 是减函数,
是减函数,
在区间![]() 上,
上,![]() ,
,![]() 是增函数,
是增函数,
故当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在长方体ABCD-A1B1C1D1中(如图),AD=AA1=1,AB=2,点E是棱AB的中点.
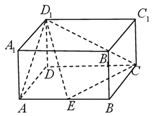
(1)求异面直线AD1与EC所成角的大小;
(2)《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,试问四面体D1CDE是否为鳖臑?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设要考察某公司生产的![]() 克袋装牛奶的质量是否达标,现从
克袋装牛奶的质量是否达标,现从![]() 袋牛奶中抽取
袋牛奶中抽取![]() 袋牛奶进行检验,利用随机数表抽样时,先将
袋牛奶进行检验,利用随机数表抽样时,先将![]() 袋牛奶按
袋牛奶按![]() 、
、![]() 、
、![]() 、
、![]() 进行编号,如果从随机数表第
进行编号,如果从随机数表第![]() 行第
行第![]() 列开始向右读,请你依次写出最先检测的
列开始向右读,请你依次写出最先检测的![]() 袋牛奶的编号_____________,_____________,_____________,_____________,_____________.(下面摘取了随机数表第
袋牛奶的编号_____________,_____________,_____________,_____________,_____________.(下面摘取了随机数表第![]() 行至第
行至第![]() 行)
行)
8842 1753 3157 2455 0688 7704 7476 7217 6335 0258 3921 2067 64
6301 6378 5916 9556 6719 9810 5071 7512 8673 5807 4439 5238 79
3321 1234 2978 6456 0782 5242 0744 3815 5100 1342 9966 0279 54
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的命题有______.
①回归直线![]() 恒过样本的中心
恒过样本的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
②若![]() ,则事件
,则事件![]() 与
与![]() 是对立事件;
是对立事件;
③一组数据的方差一定是正数;
④用系统抽样法从![]() 名学生中抽取容量为
名学生中抽取容量为![]() 的样本,将
的样本,将![]() 名学生从
名学生从![]() 编号,按编号顺序平均分成
编号,按编号顺序平均分成![]() 组(
组(![]() 号,
号,![]() 号,……,
号,……,![]() 号),若第
号),若第![]() 组抽出的号码为
组抽出的号码为![]() ,则第一组中用抽签法确定的号码为
,则第一组中用抽签法确定的号码为![]() 号.
号.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体![]() 的长,宽,高分别为4,3,5,现有一甲壳虫从
的长,宽,高分别为4,3,5,现有一甲壳虫从![]() 点出发沿长方体表面爬行到
点出发沿长方体表面爬行到![]() 点来获取食物.
点来获取食物.
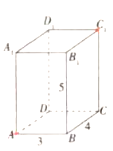
(1)甲壳虫想尽快获取食物可通过哪些路径获取?
(2)哪条获取食物的路径最短?最短为多少?
(3)此类问题的一般处理方法是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C![]() (t∈R,t≠0)为圆心的圆与x轴交于点O和点A,与y轴交于点O和点B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O和点A,与y轴交于点O和点B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y=-2x+4与圆C交于点M,N,若OM=ON,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() (底面为正三角形,侧棱和底面垂直)的所有棱长都为2,
(底面为正三角形,侧棱和底面垂直)的所有棱长都为2,![]() 为
为![]() 的中点,O为
的中点,O为![]() 中点.
中点.
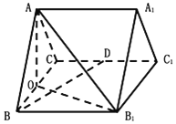
(1)求证:![]() 平面
平面![]() .
.
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com