设f(x)=3ax2-2bx+c,若a-b+c=0,f(0)>0,f(1)>0.
(1)求证:方程f(x)=0在区间(0,1)内有两个不等的实数根;
(2)若a,b,c都为正整数,求a+b+c的最小值.
证明:(1)f(0)=c>0①,
f(1)=3a-2b+c>0②,a-b+c=0③,
由①③得:a-b<0?a<b④,由②③得:2a-b>0?2a>b⑤,
由④⑤得:2a>b>a⑥,∵b=a+c代入②得:a>c∴a>0
∴由⑤得:
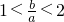
…(4分)
∵对称轴
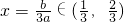
,
又f(0)>0,f(1)>0
且△=4b
2-12ac=4(a+c)
2-12ac=(2a-c)
2+3c
2>0
∴方程f(x)=0在(0,1)内有两个不等实根.…(10分)
(2)若a,b,c都为正整数,f(0)、f(1)都是正整数,
设f(x)=3a(x-x
1)(x-x
2),其中x
1,x
2是f(x)=0的两根,
则x
1,x
2∈(0,1),且x
1≠x
2∵
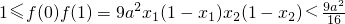
∴9a
2>16,a为正整数,
∴a≥2,
∴a+b+c≥2+(2+c)+c=4+2c≥6…(15分)
若取a=2,则
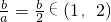
得:b∈(2,4)
∵b为正整数,∴b=3,c=b-a=1f(x)=6x
2-6x+1=0的两根都在区间(0,1)内,
∴a+b+c的最小值为6.…(18分)
分析:(1)f(0)=c>0①,f(1)=3a-2b+c>0,所以a-b+c=0,由此得:a-b<0?a<b,由2a-b>0?2a>b,2a>b>a.b=a+ca>c.方程f(x)=0在区间(0,1)内有两个不等的实数根;
(2)若a,b,c都为正整数,f(0)、f(1)都是正整数,设f(x)=3a(x-x
1)(x-x
2),由此能求出a+b+c的最小值.
点评:本题考查二次函数的综合运用,解题时要认真审题,仔细解答,注意韦达定理的合理运用.

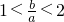 …(4分)
…(4分)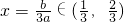 ,
,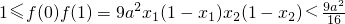
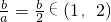 得:b∈(2,4)
得:b∈(2,4)

 阅读快车系列答案
阅读快车系列答案