
 如图,线段AB在平面α内,线段CA⊥α,线段DB⊥AB,直线DB与CA成60°,若CA=AB=BD=2,则C,D间的距离是
如图,线段AB在平面α内,线段CA⊥α,线段DB⊥AB,直线DB与CA成60°,若CA=AB=BD=2,则C,D间的距离是

科目:高中数学 来源: 题型:
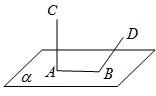 如图,线段AB在平面α内,线段CA⊥α,线段DB⊥AB,直线DB与CA成60°,若CA=AB=BD=2,则C,D间的距离是( )
如图,线段AB在平面α内,线段CA⊥α,线段DB⊥AB,直线DB与CA成60°,若CA=AB=BD=2,则C,D间的距离是( )A、2
| ||
| B、2 | ||
C、
| ||
| D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
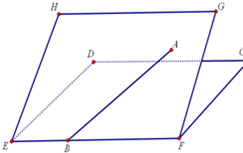 如图,二面角C-EF-G的大小是60°,线段AB在平面EFGH上,B在EF上,AB与EF所成的角为30°,则AB与平面CDEF所成的角的正弦值是
如图,二面角C-EF-G的大小是60°,线段AB在平面EFGH上,B在EF上,AB与EF所成的角为30°,则AB与平面CDEF所成的角的正弦值是查看答案和解析>>
科目:高中数学 来源: 题型:

②“线段AB在平面α内,直线AB不全在平面α内”这一说法是否正确,为什么?
③如果一条直线过平面内一点与平面外一点,那么它和这个平面有几个公共点?说明道理.
④“平面α与平面β只有一个公共点”,这一说法是否正确?说明道理.
查看答案和解析>>
科目:高中数学 来源:2011年四川省宜宾市高考数学调研试卷(文科)(解析版) 题型:选择题
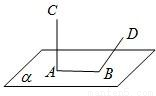


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com