
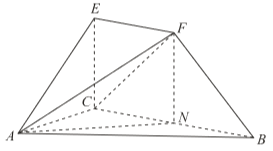
【题目】如图,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)(文科)求三棱锥![]() 的体积.
的体积.
(理科)求二面角![]() 平面角正切值的大小.
平面角正切值的大小.
【答案】(1)见解析;(2)(文科)![]() ,(理科)
,(理科)![]() .
.
【解析】分析:(1)利用线面垂直的判定定理和面面垂直的判定定理进行证明;(2)(文)借助(1)结论得到线面垂直,再利用线面角和余弦定理得到有关线段的长度,再利用等体积法进行求解;(理)借助(1)结论得到线面垂直,再利用线面角和余弦定理得到有关线段的长度,再利用线面垂直的判定和性质得到线面垂直和线线垂直,进而得到二面角的平面角,再通过解直角三角形求解.
详解:(1)证明:![]()
![]()
![]() 平面
平面![]() 平面
平面![]()
![]() 平面
平面![]() . .
. .
(2)(文科)取![]() 的中点
的中点![]() ,则
,则![]() ,连接
,连接![]() ,
,![]() .
.
∵ ![]() ,
,![]() , ∴
, ∴ ![]() ,
,![]() ,
,
∴ ![]() 平面
平面![]() ,
,
∵ 直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ,∴
,∴ ![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
∴ 在![]() 中,
中,![]() ,
,
∴ ![]() .
.
(理科)取![]() 的中点
的中点![]() ,则
,则![]() ,连接
,连接![]() ,
,![]() .
.

∵ ![]() ,
,![]() , ∴
, ∴ ![]() ,
,![]() ,
,
从而![]() 平面
平面![]() ,
,
∵ 直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() ,∴
,∴ ![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
在![]() 中,
中,![]() ,
,
作![]() 于
于![]() ,由
,由![]()
![]()
![]() 平面
平面![]()
![]()
![]() ,
,
∴ ![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,可得
中,可得![]() ,
,
在![]() 中,
中,![]() .
.


科目:高中数学 来源: 题型:
【题目】一台风中心在港口南偏东![]() 方向上,距离港口
方向上,距离港口![]() 千米处的海面上形成,并以每小时
千米处的海面上形成,并以每小时![]() 千米的速度向正北方向移动,距台风中心
千米的速度向正北方向移动,距台风中心![]() 千米以内的范围将受到台风的影响,则港口受到台风影响的时间为( )
千米以内的范围将受到台风的影响,则港口受到台风影响的时间为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V-ABC中,平面VAB![]() 平面ABC,
平面ABC, ![]() VAB为等边三角形,AC
VAB为等边三角形,AC![]() BC且AC=BC=
BC且AC=BC=![]() ,O,M分别为AB,VA的中点。
,O,M分别为AB,VA的中点。
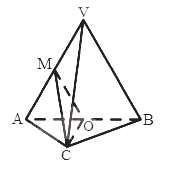
(I)求证:VB//平面MOC;
(II)求证:平面MOC![]() 平面VAB;
平面VAB;
(III)求三棱锥V-ABC的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线![]() 的方程为
的方程为![]() .
.
(![]() )在所给坐标系中画出圆锥曲线
)在所给坐标系中画出圆锥曲线![]() .
.
(![]() )圆锥曲线
)圆锥曲线![]() 的离心率
的离心率![]() __________.
__________.
(![]() )如果顶点在原点的抛物线
)如果顶点在原点的抛物线![]() 与圆锥曲线
与圆锥曲线![]() 有一个公共焦点
有一个公共焦点![]() ,且过第一象限,则
,且过第一象限,则
(i)交点![]() 的坐标为__________.
的坐标为__________.
(ii)抛物线![]() 的方程为__________.
的方程为__________.
(iii)在图中画出抛物线![]() 的准线.
的准线.
(![]() )已知矩形
)已知矩形![]() 各顶点都在圆锥曲线
各顶点都在圆锥曲线![]() 上,则矩形
上,则矩形![]() 面积的最大值为__________.
面积的最大值为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,
, ![]() 为圆
为圆![]() 上一点,线段
上一点,线段![]() 上一点
上一点![]() 满足
满足![]() ,直线
,直线![]() 上一点
上一点![]() ,满足
,满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 为坐标原点,
为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹
相切,并与轨迹![]() 交于不同的两点
交于不同的两点![]() .当
.当![]() 且满足
且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业里工人的工资与其生产利润满足线性相关关系,现统计了100名工人的工资![]() (元)与其生产利润
(元)与其生产利润![]() (千元)的数据,建立了
(千元)的数据,建立了![]() 关于
关于![]() 的回归直线方程为
的回归直线方程为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 工人甲的生产利润为1000元,则甲的工资为130元
B. 生产利润提高1000元,则预计工资约提高80元
C. 生产利润提高1000元,则预计工资约提高130元
D. 工人乙的工资为210元,则乙的生产利润为2000元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com