
分析 (1)根据题意,由抛物线的定义,可得$2+\frac{p}{2}=3$,解可得p=2,代入标准方程,即可得答案;
(2)联立直线与抛物线的方程,消去y得x2-6x+1=0,进而设A(x1,y1),B(x2,y2),由一元二次方程根与系数的关系可得x1+x2=6,结合抛物线的几何性质,可得|AB|的长,由点到直线距离公式可得O到直线y=x-1,进而由三角形面积公式计算可得答案.
解答 解:(1)根据题意,D(2,y0)在抛物线y2=2px,上且|DF|=3
由抛物线定义得$2+\frac{p}{2}=3$,∴p=2
故抛物线的方程为y2=4x;
(2)由方程组$\left\{\begin{array}{l}y=x-1\\{y^2}=4x\end{array}\right.$,消去y得x2-6x+1=0,
设A(x1,y1),B(x2,y2),则x1+x2=6;
∵直线y=x-1过抛物线y2=4x的焦点F,
∴|AB|=x1+x2+p=6+2=8
又O到直线y=x-1的距离$d=\frac{{\sqrt{2}}}{2}$,
∴△ABO的面积$S=\frac{1}{2}|AB|d=2\sqrt{2}$.
点评 本题考查抛物线的几何性质,涉及直线与抛物线的位置关系,关键是利用抛物线的几何性质求出其标准方程.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
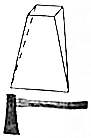 斧头的形状叫楔形,在《算数书》中又称之为“郓(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一线段.有一斧头:上厚为三,下厚为六,高为五及袤(m$\stackrel{、}{a}$o)为二,问此斧头的体积为几何?意思就是说有一斧头形的几何体,上底为矩形,下底为一线段,上底的长为3,下底线段长为6,上下底间的距离(高)为5,上底矩形的宽为2,则此几何体的体积是( )
斧头的形状叫楔形,在《算数书》中又称之为“郓(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一线段.有一斧头:上厚为三,下厚为六,高为五及袤(m$\stackrel{、}{a}$o)为二,问此斧头的体积为几何?意思就是说有一斧头形的几何体,上底为矩形,下底为一线段,上底的长为3,下底线段长为6,上下底间的距离(高)为5,上底矩形的宽为2,则此几何体的体积是( )| A. | 6 | B. | 10 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x+2013 | B. | f(x)=-x+2013 | C. | f(x)=-x-2013 | D. | f(x)=x-2013 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 1 | B. | $\sqrt{2015}$-1 | C. | $\sqrt{2016}$-1 | D. | $\sqrt{2017}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
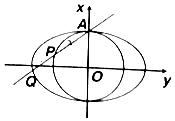 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆O:x2+y2=b2,过椭圆C的上顶点A的直线l:y=kx+b分别交圆O、椭圆C于不同的两点P、Q,设$\overrightarrow{AP}$=λ$\overrightarrow{PQ}$.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆O:x2+y2=b2,过椭圆C的上顶点A的直线l:y=kx+b分别交圆O、椭圆C于不同的两点P、Q,设$\overrightarrow{AP}$=λ$\overrightarrow{PQ}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com