已知集合A={(x,y)|(3+m)x+y=2m},B={(x,y)|7x+(5-m)y=8},若A∩B=∅,求直线(3+m)x+y=3m+4与两坐标轴所围成的三角形的面积.
解:根据A∩B=∅,得两条直线(3+m)x+y=2m,7x+(5-m)y=8平行;
当m=5时,两直线的方程为8x+y=10;7x=8不合题意;
当m≠5时,要使直线(3+m)x+y=2m,7x+(5-m)y=8平行,需-(3+m)=
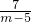
≠

解得m=-2.
∴直线(3+m)x+y=3m+4即:x+y=-2.
当x=0时,y=-2,
当y=0时,x=-2,
∴所求三角形的面积
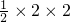
=2.
分析:根据A∩B=∅,得两条直线平行,列出关系,求出m的范围.易得此直线与坐标轴的两个交点坐标,与坐标轴围成的三角形的面积等于

×与x轴交点的横坐标×与y轴交点的纵坐标的绝对值.
点评:本题考查两条直线平行的关系、三角形的面积公式,是基础题.

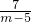 ≠
≠
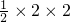 =2.
=2. ×与x轴交点的横坐标×与y轴交点的纵坐标的绝对值.
×与x轴交点的横坐标×与y轴交点的纵坐标的绝对值.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案