【题目】已知函数
．
（1）若
，求a的取值范围；
（2）
，
，求a的取值范围．
【答案】(1) 
．(2) 
．
【解析】
（1）f（1）＝|2a+1|﹣|a﹣1|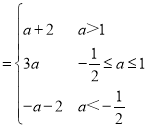
，根据f（1）＞2分别解不等式即可'
（2）根据绝对值三角不等式求出f（x）的值域，然后由条件可得f（x）min＞f（y）max﹣6，即﹣3|a|＞3|a|﹣6，解出a的范围．
（1）∵f（x）＝|x+2a|﹣|x﹣a|，
∴f（1）＝|2a+1|﹣|a﹣1|，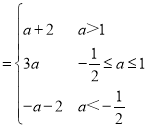
∵f（1）＞2，∴
，或
，或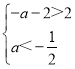
，
∴a＞1，或
a≤1，或a＜﹣4，
∴a的取值范围为
；
（2）∵||x+2a|﹣|x﹣a||≤|（x+2a）﹣（x﹣a）|＝3|a|，
∴f（x）∈[﹣3|a|，3|a|]，
∵x、y∈R，f（x）＞f（y）﹣6，
∴只需f（x）min＞f（y）max﹣6，即﹣3|a|＞3|a|﹣6，
∴6|a|＜6，∴﹣1＜a＜1，
∴a的取值范围为[﹣1，1]．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x|x-a|+bx（a，b∈R）．
（Ⅰ）当b=-1时，函数f（x）恰有两个不同的零点，求实数a的值；
（Ⅱ）当b=1时，
①若对于任意x∈[1，3]，恒有f（x）≤2x2，求a的取值范围；
②若a≥2，求函数f（x）在区间[0，2]上的最大值g（a）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】用
分别表示
的三个内角
所对边的边长，
表示的外接圆半径.
（1）
，求
的长；
（2）在中，若
是钝角，求证：
；
（3）给定三个正实数
，其中
，问满足怎样的关系时，以
为边长，为外接圆半径的不存在，存在一个或存在两个（全等的三角形算作同一个）？在存在的情况下，用表示
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在△
中，
,
分别为
，
的中点，
为
的中点， 
，
．将△
沿折起到△
的位置，使得平面
平面
， 
为
的中点，如图2．
（Ⅰ）求证： 
平面
；
（Ⅱ）求F到平面A1OB的距离．
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
