
【题目】已知函数![]() ,
, ![]() .
.
(1)证明: ![]() ,直线
,直线![]() 都不是曲线
都不是曲线![]() 的切线;
的切线;
(2)若![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)若直线![]() 与曲线
与曲线![]() 相切,因直线
相切,因直线![]() 过定点
过定点![]() ,若设切点
,若设切点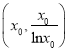 则可得
则可得![]() ①,又
①,又![]() ,
, ![]() 上单调递增,当且仅当
上单调递增,当且仅当![]() 时,①成立,这与
时,①成立,这与![]() 矛盾,结论得证.
矛盾,结论得证.
(2)![]() 可转化为
可转化为![]() ,令
,令![]() ,
, ![]() ,
, ![]() ,分类讨论求
,分类讨论求![]() 的最小值即可.
的最小值即可.
试题解析: (1)![]() 的定义域为
的定义域为![]() ,
, ![]() ,直线
,直线![]() 过定点
过定点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切于点
相切于点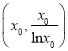 (
(![]() 且
且![]() ),则
),则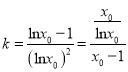 ,即
,即![]() ①,设
①,设![]() ,
, ![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,从而当且仅当
,从而当且仅当![]() 时,①成立,这与
时,①成立,这与![]() 矛盾.
矛盾.
所以, ![]() ,直线
,直线![]() 都不是曲线
都不是曲线![]() 的切线;
的切线;
(2)![]() 即
即![]() ,令
,令![]() ,
, ![]() ,
,
则![]() ,使
,使![]() 成立
成立![]() ,
,
 .
.
(i)当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为减函数,于是
上为减函数,于是![]() ,由
,由![]() 得
得![]() ,满足
,满足![]() ,所以
,所以![]() 符合题意;
符合题意;
(ii)当![]() 时,由
时,由![]() 及
及![]() 的单调性知
的单调性知![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() ,即
,即![]() .
.
①若![]() ,即
,即![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 为增函数,于是
为增函数,于是![]() ,不合题意;
,不合题意;
②若![]() ,即
,即![]() ,则由
,则由![]() ,
, ![]() 及
及![]() 的单调性知存在唯一
的单调性知存在唯一![]() ,使
,使![]() ,且当
,且当![]() 时,
时, ![]() ,
, ![]() 为减函数;当
为减函数;当![]() 时,
时, ![]() ,
, ![]() 为增函数;
为增函数;
所以![]() ,由
,由![]() 得
得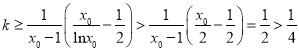 ,这与
,这与![]() 矛盾,不合题意.
矛盾,不合题意.
综上可知, ![]() 的取值范围是
的取值范围是![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为![]() ,短轴长为
,短轴长为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相切,探究
相切,探究![]() 是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内一动点![]() 与两定点
与两定点![]() 和
和![]() 连线的斜率之积等于
连线的斜率之积等于![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设直线![]() :
: ![]() (
(![]() )与轨迹
)与轨迹![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,当
,当![]() 变化时,求
变化时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)是否存在实数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)( ![]() )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点 ![]() 对称
对称
B.关于点 ![]() 对称
对称
C.关于直线 ![]() 对称
对称
D.关于直线 ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节来临,有农民工兄弟![]() 、
、![]() 、
、![]() 、
、![]() 四人各自通过互联网订购回家过年的火车票,若订票成功即可获得火车票,即他们获得火车票与否互不影响.若
四人各自通过互联网订购回家过年的火车票,若订票成功即可获得火车票,即他们获得火车票与否互不影响.若![]() 、
、![]() 、
、![]() 、
、![]() 获得火车票的概率分别是
获得火车票的概率分别是![]() ,其中
,其中![]() ,又
,又![]() 成等比数列,且
成等比数列,且![]() 、
、![]() 两人恰好有一人获得火车票的概率是
两人恰好有一人获得火车票的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 、
、![]() 是一家人且两人都获得火车票才一起回家,否则两人都不回家.设
是一家人且两人都获得火车票才一起回家,否则两人都不回家.设![]() 表示
表示![]() 、
、![]() 、
、![]() 、
、![]() 能够回家过年的人数,求
能够回家过年的人数,求![]() 的分布列和期望
的分布列和期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com