
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ABB1A1是菱形,且CA=CB1.
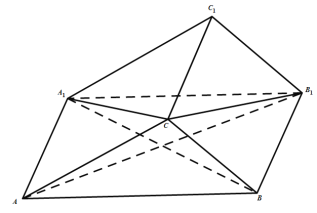
(1)证明:面CBA1⊥面CB1A;
(2)若∠BAA1=60°,A1C=BC=BA1,求二面角C﹣A1B1﹣C1的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设AB1与A1B交于O,连接OC,先证明AB1⊥平面CA1B,再根据面面垂直的判定定理即可得证;
(2)由A1C=BC,故CO⊥A1B,又(1)知OC⊥AB1,AB1∩A1B=O,故OC⊥平面ABB1A1,以O为原点,分别以OA,OB,OC为x,y,z轴建立空间直角坐标系,求出平面CA1B1和平面C1A1B1的法向量,利用夹角公式求出即可.
(1)证明:设AB1与A1B交于O,连接OC,如图,
因为侧面ABB1A1是菱形,所以AB1⊥A1B,
又CA=CB1,所以OC⊥AB1,又A1B∩CO=O,
故AB1⊥平面CA1B,又AB1平面CAB1,
故平面CBA1⊥平面CB1A;

(2)由A1C=BC,故CO⊥A1B,又(1)知OC⊥AB1,AB1∩A1B=O,
故OC⊥平面ABB1A1,以O为原点,分别以OA,OB,OC为x,y,z轴建立空间直角坐标系,如图,
设A1C=BC=BA1=2,则OC![]() ,
,
则![]() ,
,![]() ,A1(0,﹣1,0),B(0,1,0),
,A1(0,﹣1,0),B(0,1,0),
由![]() ,得
,得![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设平面CA1B1的一个法向量为![]() ,
,
由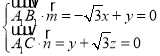 ,得
,得![]() ,
,
设平面C1A1B1的一个法向量为![]() ,
,
由 ,得
,得 ![]() ,
,
故cos![]() ,
,
又二面角C﹣A1B1﹣C1为锐角,
故二面角C﹣A1B1﹣C1的余弦值为![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的左右两个焦点,过
的左右两个焦点,过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在第一象限),
在第一象限),![]() 的周长为8,
的周长为8,![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() ,
,![]() 为
为![]() 的左右顶点,直线
的左右顶点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知椭圆C:![]() 的离心率为
的离心率为![]() ,且点
,且点![]() 在椭圆C上.椭圆C的左顶点为A.
在椭圆C上.椭圆C的左顶点为A.
(1)求椭圆C的方程
(2)椭圆的右焦点且斜率为![]() 的直线与椭圆交于P,Q两点,求三角形APQ的面积;
的直线与椭圆交于P,Q两点,求三角形APQ的面积;
(3)过点A作直线与椭圆C交于另一点B.若直线![]() 交
交![]() 轴于点C,且
轴于点C,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着2022年北京冬奥会的临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放.如图是2012-2018年中国雪场滑雪人数(单位:万人)与同比增长情况统计图.则下面结论中正确的是( )
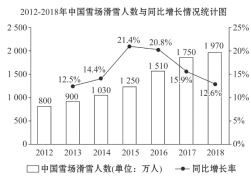
①2012-2018年,中国雪场滑雪人数逐年增加;②2013-2015年,中国雪场滑雪人数和同比增长率均逐年增加;③中国雪场2015年比2014年增加的滑雪人数和2018年比2017年增加的滑雪人数均为220万人,因此这两年的同比增长率均有提高;④2016-2018年,中国雪场滑雪人数的增长率约为23.4%.
A.①②③B.②③④C.①②D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在创建“全国文明卫生城市”的过程中,为了调查市民对创建“全国文明卫生城市”工作的了解情况,进行了一次知识问卷调查(一位市民只能参加一次).通过随机抽样,得到参加问卷调查的1000人的得分(满分100分)统计结果如下表所示.
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)该市把得分不低于80分的市民称为“热心市民”,若以频率估计概率,以样本估计总体,求从该市的市民中任意抽取一位,抽到“热心市民”的概率;
(2)由频数分布表可以大致认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组数据区间的中点值表示),请用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组数据区间的中点值表示),请用正态分布的知识求![]() ;
;
(3)在(2)的条件下,该市为此次参加问卷调查的市民制定如下奖励方案:
(ⅰ)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ⅱ)每次获赠送的随机话费和对应的概率为:
赠送的随机话费(单元:元) | 30 | 60 |
概率 | 0.75 | 0.25 |
现有市民甲要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:参考数据与公式
![]() ,若
,若![]() ,则①
,则①![]() ;
;
②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x+b|,ab>0.
(1)当a=1,b=1时,求不等式f(x)<3的解集;
(2)若f(x)的最小值为2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,全国各地区坚持稳中求进工作总基调,经济运行总体平稳,发展水平迈上新台阶,发展质量稳步上升,人民生活福祉持续增进,全年最终消费支出对国内生产总值增长的贡献率为57.8%.下图为2019年居民消费价格月度涨跌幅度:(同比![]() (本期数-去年同期数)/去年同期数
(本期数-去年同期数)/去年同期数![]() ,环比
,环比![]() (本期数-上期数)/上期数
(本期数-上期数)/上期数![]()

下列结论中不正确的是( )
A.2019年第三季度的居民消费价格一直都在增长
B.2018年7月份的居民消费价格比同年8月份要低一些
C.2019年全年居民消费价格比2018年涨了2.5%以上
D.2019年3月份的居民消费价格全年最低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学长期坚持贯彻以人为本,因材施教的教育理念,每年都会在校文化节期间举行“数学素养能力测试”和“语文素养能力测试”两项测试,以给学生课外兴趣学习及辅导提供参考依据.成绩分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级(等级
五个等级(等级![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别对应5分,4分,3分,2分,1分).某班学生两科的考试成绩的数据统计如图所示,其中“语文素养能力测试”科目的成绩为
分别对应5分,4分,3分,2分,1分).某班学生两科的考试成绩的数据统计如图所示,其中“语文素养能力测试”科目的成绩为![]() 的考生有3人.
的考生有3人.
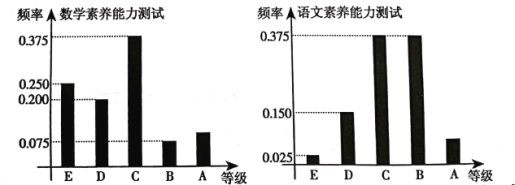
(1)求该班“数学素养能力测试”的科目平均分以及“数学素养能力测试”科目成绩为![]() 的人数;
的人数;
(2)若该班共有9人得分大于7分,其中有2人10分,3人9分,4人8分.从这9人中随机抽取三人,设三人的成绩之和为![]() ,求
,求![]() .
.
(3)从该班得分大于7分的9人中选3人即甲,乙,丙组队参加学校内的“数学限时解题挑战赛”.规则为:每队首先派一名队员参加挑战赛,在限定的时间,若该生解决问题,即团队挑战成功,结束挑战;若解决问题失败,则派另外一名队员上去挑战,直至派完队员为止.通过训练,已知甲,乙,丙通过挑战赛的概率分别是![]() ,
,![]() ,
,![]() ,问以怎样的先后顺序派出队员,可使得派出队员数目的均值达到最小?(只需写出结果)
,问以怎样的先后顺序派出队员,可使得派出队员数目的均值达到最小?(只需写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的棱长均为6,其内有
的棱长均为6,其内有![]() 个小球,球
个小球,球![]() 与三棱锥
与三棱锥![]() 的四个面都相切,球
的四个面都相切,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切,如此类推,…,球
都相切,如此类推,…,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切(
都相切(![]() ,且
,且![]() ),则球
),则球![]() 的体积等于__________,球
的体积等于__________,球![]() 的表面积等于__________.
的表面积等于__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com