
【题目】对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为 . 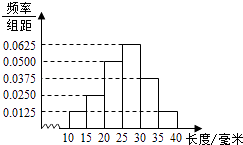
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】设{an}是公比为正整数的等比数列,{bn}是等差数列,且a1a2a3=64,b1+b2+b3=﹣42,6a1+b1=2a3+b3=0.
(1)求数列{an}和{bn}的通项公式;
(2)设pn= ![]() ,数列{pn}的前n项和为Sn .
,数列{pn}的前n项和为Sn .
①试求最小的正整数n0 , 使得当n≥n0时,都有S2n>0成立;
②是否存在正整数m,n(m<n),使得Sm=Sn成立?若存在,请求出所有满足条件的m,n;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.

(1)试根据所给数据计算每小时点击次数的均值方差并分析两组数据的特征;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为![]() ,则点
,则点![]() 近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线
近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: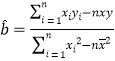 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣3,数列{bn}的前n项和Tn满足 ![]() =
= ![]() +1且b1=1.
+1且b1=1.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前n项和Pn;
,求数列{cn}的前n项和Pn;
(3)数列{Sn}中是否存在不同的三项Sp , Sq , Sr , 使这三项恰好构成等差数列?若存在,求出p,q,r的关系;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() x+y﹣
x+y﹣ ![]() =0经过椭圆C:
=0经过椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点和上顶点.
=1(a>b>0)的右焦点和上顶点.
(1)求椭圆C的标准方程;
(2)过点(0,﹣2)的直线l与椭圆C交于不同的A,B两点,若∠AOB为钝角,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若 ![]() ,
, ![]() ,
, ![]() 为同一平面内互不共线的三个单位向量,并满足
为同一平面内互不共线的三个单位向量,并满足 ![]() +
+ ![]() +
+ ![]() =
= ![]() ,且向量
,且向量 ![]() =x
=x ![]() +
+ ![]()
![]() +(x+
+(x+ ![]() )
) ![]() (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求 ![]() 与
与 ![]() 所成角的大小;
所成角的大小;
(2)记f(x)=| ![]() |,试求f(x)的单调区间及最小值.
|,试求f(x)的单调区间及最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com