
【题目】设椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与
的直线与![]() 交于点
交于点![]() ,
,![]() . 若
. 若![]() ,且
,且![]() ,则
,则![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
由题意画出图形,由|PF2|=|F1F2|,3|PF1|=4|QF1|,利用椭圆的定义可得:|PF1|=2a﹣2c,进一步求出|QF1|,|QF2|,在等腰△PF1F2中,求得得cos∠PF1F2.在△QF1F2中,由余弦定理可得cos∠QF1F2,利用cos∠PF1F2+cos∠QF1F2=0,化简求得5a=7c,两边平方后结合隐含条件求得![]() 的值,则C的离心率可求.
的值,则C的离心率可求.
如图所示,
∵|PF2|=|F1F2|,
∴|PF2|=2c,则|PF1|=2a﹣2c.
∵3|PF1|=4|QF1|,
∴|QF1|![]() (2a﹣2c)
(2a﹣2c)![]() (a﹣c),
(a﹣c),
则|QF2|=2a![]() (a﹣c)
(a﹣c)![]() c.
c.
在等腰△PF1F2中,可得cos∠PF1F2![]() .
.
在△QF1F2中,由余弦定理可得: ,
,
由cos∠PF1F2+cos∠QF1F2=0,得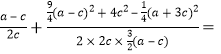 0,
0,
整理得:![]() ,∴5a=7c,
,∴5a=7c,
则25a2=49c2=49(a2﹣b2),
∴![]() .
.
则![]() .
.
故选:A.


科目:高中数学 来源: 题型:
【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 是以原点O为中心、
是以原点O为中心、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以O为顶点、
是以O为顶点、![]() 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线![]() 和
和![]() 的交点且
的交点且![]() 为钝角,若
为钝角,若![]() ,
,![]() .
.

(1)求曲线![]() 和
和![]() 的方程;
的方程;
(2)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问![]() 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=AC=1,BB1=2,∠ABB1=60°.
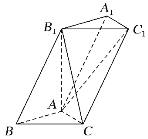
(I) 证明:AB⊥平面AB1C;
(II) 若B1C=2,求AC1与平面BCB1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.

(Ⅰ) 求证:OC⊥PD;
(II)若PD与平面PAB所成的角为30°,求二面角D-PC-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.在党和政府强有力的抗疫领导下,我国控制住疫情后,一方面防止境外疫情输入,另一方面逐步复工复产,减轻经济下降对企业和民众带来的损失.为降低疫情影响,某厂家拟在2020年举行某产品的促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按
为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按![]() 元来计算)
元来计算)
(1)将2020年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com