
【题目】某城市地铁项目正在紧张建设中,通车后将给市民出行带来便利.已知某条线路通车后,地铁的发车时间间隔![]() (单位:分钟)满足
(单位:分钟)满足![]() .经测算,地铁载客量与发车时间间隔
.经测算,地铁载客量与发车时间间隔![]() 相关,当
相关,当![]() 时地铁为满载状态,载客量为
时地铁为满载状态,载客量为![]() 人,当
人,当![]() 时,载客量会减少,减少的人数与
时,载客量会减少,减少的人数与![]() 的平方成正比,且发车时间间隔为
的平方成正比,且发车时间间隔为![]() 分钟时的载客量为
分钟时的载客量为![]() 人,记地铁载客量为
人,记地铁载客量为![]() .
.
(1)求![]() 的表达式,并求当发车时间间隔为
的表达式,并求当发车时间间隔为![]() 分钟时,地铁的载客量;
分钟时,地铁的载客量;
(2)若该线路每分钟的净收益为![]() (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?每分钟的最大净收益为多少?
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?每分钟的最大净收益为多少?
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知距离为![]() 的
的![]() 、
、![]() 两点在直线
两点在直线![]() 的同侧,且
的同侧,且![]() 、
、![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() 、
、![]() .问能否作出经过
.问能否作出经过![]() 、
、![]() 两点且与直线
两点且与直线![]() 相切的圆?若能,请写出作法,画图并求出圆的半径;若不能,说明理由.
相切的圆?若能,请写出作法,画图并求出圆的半径;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入冬天,大气流动性变差,容易形成雾握天气,从而影响空气质量.某城市环保部门试图探究车流量与空气质量的相关性,以确定是否对车辆实施限行.为此,环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表:

(1)根据表中周一到周五的数据,求y关于x的线性回归方程。
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是可靠的.请根据周六和周日数据,判定所得的线性回归方程是否可靠?
注:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C的参数方程是![]() (θ为参数).以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为:
(θ为参数).以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为:![]()
(1)求曲线C的极坐标方程;
(2)设直线θ=![]() 与直线l交于点M,与曲线C交于P,Q两点,已知|OM||OP||OQ)=10,求t的值。
与直线l交于点M,与曲线C交于P,Q两点,已知|OM||OP||OQ)=10,求t的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1,中,点M是棱BC的中点.
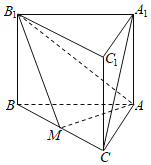
(2)求证:A1C∥平面AB1M;
(2)如果AB=AC,求证AM⊥平面BCC1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
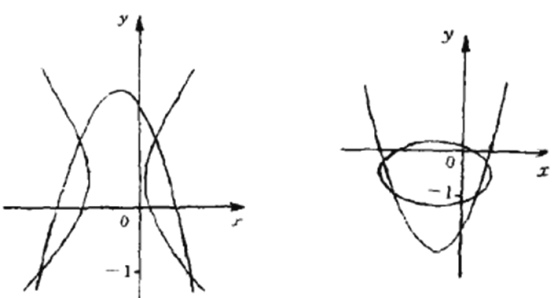
【题目】已知抛物线![]() 与二次曲线
与二次曲线![]() 有4个不同的交点,由下面的草图可以看出,下面三个结论是成立的,请给出证明.
有4个不同的交点,由下面的草图可以看出,下面三个结论是成立的,请给出证明.
(1).两曲线的4个交点中,至少有两个交点位于![]() 轴的下方;
轴的下方;
(2).抛物线![]() 必与
必与![]() 轴有两个不同的交点,记为
轴有两个不同的交点,记为![]() ,
,![]() ,
,![]() ;
;
(3).两曲线的4个交点中,必存在一点![]() ,使
,使![]() .
.
注.对![]() 、
、![]() 、
、![]() 的不同取值会有无数个图形,此处仅就
的不同取值会有无数个图形,此处仅就![]() ,
,![]() 各给出一个示意图,同时也就限制“由图看出”的解答.
各给出一个示意图,同时也就限制“由图看出”的解答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com